Algoritmos computacionales

La solución matemática de cualquier problema del orden científico requiere forzosamente que se proporcione algún procedimiento que mediante una serie finita de pasos conduzca a una solución ya sea exacta o al menos aproximada, de lo contrario el problema es insoluble. El procedimiento no puede ser ambigüo ni dependiente de la intuición o corazonadas, debe poder ser expresado de modo riguroso y formal para poder ser aplicado al pie de la letra como si fuese una “receta de cocina”, y de hecho estamos hablando de lo que puede ser llamado una receta numérica. La enunciación de tal “receta de cocina” es lo que se conoce como un algoritmo. Un algoritmo se puede aplicar manualmente con la ayuda de una calculadora de bolsillo, pero para cálculos laboriosos y pesados se vuelve deseable recurrir a una computadora. Esta necesidad fue precisamente lo que dió origen a la creación y el desarrollo de las computadoras digitales.

Frecuentemente se encuentran problemas para cuya solución numérica existen varias maneras de obtener la respuesta, y hablando en términos de eficiencia computacional puede haber algunas maneras que son mucho más rápidas que otras aunque todas proporcionen la misma respuesta con la misma precisión. Un ejemplo relevante de ello es la evaluación de un polinomio dado por la siguiente expresión:

A primera vista, si queremos evaluar el polinomio para x.=.1.5, parece que lo lógico sería usar el polinomio tal cual sin cambio alguno. La evaluación numérica requerirá de una exponenciación a una cuarta potencia, o sea tres multiplicaciones, más una multiplicación adicional por el factor 3.6; y requerirá una exponenciación  a una tercera potencia, o sea dos multiplicaciones, y una multiplicación adicional por un factor de 5.9, y así sucesivamente. En total, se requieren diez multiplicaciones más cuatro adiciones.

Sin embargo, hay una forma más eficiente de llevar a cabo los cálculos, si recurrimos a un poco de álgebra para escribir lo anterior en la siguiente forma alterna:

Esto sigue requiriendo de cuatro adiciones, pero solo requiere de cuatro multiplicaciones en lugar de diez, o sea menos de la mitad de las multiplicaciones requeridas en la expresión anterior, y si tomamos en cuenta que es precisamente en las multiplicaciones en donde se consume más tiempo de operaciones aritméticas, podemos ver que en los tiempos previos a la invención de las calculadoras electrónicas cuando todos los cálculos se tenían que hacer a mano el segundo procedimiento era mil veces preferible al primero. E inclusive en los tiempos modernos cuando se cuenta con calculadoras electrónicas y computadoras de escritorio, si vamos a evaluar el polinomio anterior varios cientos de veces (o varios miles de veces) para obtener los datos para hacer una o varias gráficas Cartesianas del polinomio, la segunda alternativa es superior a la primera.

En las ciencias de la computación, abundan los casos y ejemplos de problemas que encuentran su solución mediante procedimientos que se llevan a cabo aplicando una serie de pasos ejecutados al pie de la letra aunque la razón del por qué tales procedimientos siempre funcionan no sea del todo claro para quienes los utilizan. La enseñanza de los primeros algoritmos que aprende un estudiante no empieza en la universidad, de hecho empieza desde la misma escuela primaria. Un problema clásico de la aritmética es la extracción de la raíz cuadrada de un número, por ejemplo:

√58937 = 242.7694

La extracción de la raíz cuadrada de un número como 58937 (y supondremos que se trata de un número que no tiene raíz cuadrada exacta, esto es, un entero cuyo cuadrado sea igual al número al que se le extrae raíz cuadrada) se puede llevar a cabo mediante un procedimiento o algoritmo como el que en tiempos previos se enseñaba en todas las escuelas secundarias y que por alguna razón nunca fue bien explicado en la gran mayoría de las escuelas (quizá porque muchos maestros si no todos intentaban que los alumnos aprendieran mecánicamente el procedimiento de extracción de raíces cuadradas sin explicarles jamás el por qué funcionaba el método, recurriendo a la memoria en lugar de recurrir a la comprensión). Uno de los algoritmos más frecuentemente enseñados en muchas escuelas primarias y secundarias de México, conocido en México como el “método del Profesor Chema”, es el siguiente (usaremos como referencia el ejemplo tomado del libro Matemáticas actualizadas: Primer curso del Profesor Normalista José María Sánchez Meza):

1. Se divide el número (de derecha a izquierda) en períodos de dos cifras de derecha a izquierda (el último período de la izquierda puede constar de una cifra):

58937 = 5,89,37

2. Se le saca la raíz cuadrada al primer período (ignorando fracciones decimales en caso de que las haya):

√5 = 2....

3. Se saca el primer residuo, restando del primer período el cuadrado de la raíz encontrada:

5 - 2² = 1

4. Se baja el siguiente período a continuación del primer residuo y se duplica la raíz.

5. Separando una cifra del número formado por el primer residuo y el segundo período (189), se divide entre el duplo de la raíz. El cociente se escribe en tres lugares, que son: (a) a continuación de la primera cifra de la raíz, (b) junto al duplo de la raíz, (c) para multiplicar el número formado con el duplo de la raíz.

6. El producto se resta para encontrar el segundo residuo.

7. Se baja el siguiente período, se duplica la raíz y se repiten los pasos 5 y 6 hasta terminar.

Para beneficio de aquellos cuya educación secundaria no cubrió con suficiente claridad el tema de la extracción de la raíz cuadrada de un número, a continuación se presenta un gráfico animado:

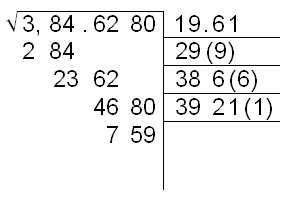
PROBLEMA: Obténgase a mano, sin la ayuda de una calculadora de bolsillo y usando el “método del Profesor Chema”, la raíz cuadrada del número 384.628.

Procediendo del mismo modo que con el ejemplo anterior, el desarrollo completo muestra el siguiente aspecto:

El procedimiento anterior es un algoritmo probado y seguro que nunca falla y siempre nos regresará con la precisión deseada la raíz cuadrada de un número. Pero no es la única manera que hay para obtener la raíz cuadrada de un número, hay otras. Una de ellas consiste en recurrir a un procedimiento iterativo. Para ilustrar dicho método, recurriremos a un ejemplo consignado en el libro Calculator Calculus del Profesor George McCarthy. El problema consiste en obtener la raíz cuadrada del número 67.89. Supondremos que tenemos a la mano una calculadora de bolsillo que no cuenta con una tecla para la extracción de la raíz cuadrada.

El primer paso para obtener la raíz cuadrada deseada, o sea √67.89, consiste en comenzar “al tanteo” con una suposición cercana a la respuesta, y puesto que 8² es igual a 64, un número que está cercano a 67.89, tomaremos tal valor como nuestro punto de partida.

El siguiente paso consiste en mejorar nuestro tanteo, y para ello recurriremos a un truco matemático. Sea y el número que estamos tratando de encontrar, de modo tal que y² = 67.89. Esto nos permite empezar con lo siguiente:

 y² = 67.89

El truco consiste en llevar a cabo la siguiente secuencia de pasos (desde el punto de vista algebraico, todos los pasos son correctos):

La ecuación que se ha obtenido solo puede ser satisfecha por y y por ningún otro número. Puesto que queremos mejorar nuestra suposición al tanteo para √67.89, haremos un experimento suponiendo que las dos apariciones del número y en esta última ecuación, o sea el y que aparece en el lado izquierdo de la igualdad y el y que aparece en el lado derecho son dos números diferentes. Le pondremos al y que aparece en el lado derecho el sub-índice 0, y le pondremos al y que aparece en el lado izquierdo el sub-índice 1. La fórmula toma entonces el siguiente aspecto:

A continuación, reemplazamos nuestra primera aproximación de y₀.=.8.0 en el lado derecho de la fórmula anterior. Si hacemos tal cosa con nuestra calculadora de bolsillo, sumándole 8 a  y₀ para obtener 16, tomando tras esto el recíproco 1/16 para obtener 0.0625, multiplicando este recíproco por 3.89 para obtener 0.243125 y finalmente sumándole a esto 8, obtenemos y₁.=.8.243125. Ahora bien, nuestra primera aproximación a la raíz cuadrada de 67.89 era 8, cuyo cuadrado es igual a 64. Por su parte, el cuadrado de y₁.=.8.243125 es 67.949110, que tampoco es la raíz cuadrada de 67.89, pero que sin embargo es una mejor aproximación a la respuesta correcta que y₀. Alentados por este hecho, escribimos la siguiente fórmula para obtener una nueva estimación:

para obtener una segunda aproximacióny₂. Puesto que y₁ aún está siendo mostrado por la calculadora de bolsillo, simplemente le sumamos 8, tomamos el recíproco, multiplicamos por 3.89 y sumando de nuevo 8. Esta es una aproximación aún más cercana, puesto que el cuadrado de y₂ es 67.889128. Podemos repetir el procedimiento de nuevo, suponiendo la validez de la fórmula iterativa:

calculando y₃ de y₂, y más generalmente y_i+1 de y_i de acuerdo a la regla anterior. Los resultados tabulares son los siguientes:

Obsérvese que y₅ = y₄  exactamente. Esto implica que:

y₅ = y₆

y₆ = y₇

y así sucesivamente. De este modo, nuestro método no puede mejorar aún más nuestra estimación final, pero ya ha hecho su trabajo.  Podemos escribir la raíz cuadrada de 68.9 como  8.2395388. Y como un chequeo final podemos comprobar en la misma calculadora que el cuadrado de 8.2395388 es 68.9 “exactamente” dentro de la precisión numérica de la calculadora (un número que no tiene raíz cuadrada exacta es un número irracional requiriendo una secuencia infinita de dígitos numéricos para escribirlo en su totalidad, lo cual no es posible ni siquiera en principio).

El método que acaba de ser descrito para obtener la raíz cuadrada del número 68.9 cae dentro de algo a lo que se le puede dar el nombre de método de aproximaciones sucesivas. El método en este caso puede ser generalizado para obtener el algoritmo que podemos usar para la evaluación de la raíz cuadrada de cualquier número x. Como antes, buscamos un número positivo y tal que  y².=.x. Si partimos de una estimación inicial e para y podemos escribir lo siguiente:

Como antes, consideramos las dos apariciones de y en esta última ecuación como dos números diferentes, o sea y_i+1 y y_i para obtener así el siguiente algoritmo:

El procedimiento que se acaba de dar para obtener la raíz cuadrada de un número con la ayuda de una calculadora ordinaria de bolsillo puede parecer superfluo porque aunque la calculadora carezca de una tecla para obtener raíces cuadradas ciertamente con una inversión mínima podemos obtener una calculadora que tenga tal tecla. ¿Pero qué puede decirse de algo como la extracción de raíces cúbicas? Por regla general, las calculadoras de bolsillo no incluyen tal tecla, para la evaluación de raíces cúbicas es necesario adquirir una calculadora científica de bolsillo. Veremos más adelante cómo se puede obtener con la ayuda de una simple calculadora de bolsillo con funciones elementales la raíz cúbica de un número cualesquiera.

Las calculadoras de bolsillo no van más allá de la obtención de la raíz cuadrada de un número, y para otras tareas más sofisticadas es necesario entrar en los detalles algorítmicos para la obtención de soluciones numéricas. Considérese la siguiente fórmula:

Supóngase que queremos encontrar una raíz del polinomio, esto es, un valor de x para el cual f(x) sea igual a cero. ¿Cómo podemos desarrollar un algoritmo para tal cosa? En realidad, no se requiere de mucha innovación. Un valor en el cual el polinomio sea igual a cero debe cumplir con la condición:

De nueva cuenta, vamos a factorizar del modo siguiente:

Esto lo podemos escribir de la siguiente manera:

Haremos ahora otro experimento suponiendo que las dos apariciones del número x en esta última ecuación, o sea el x que aparece en el lado izquierdo de la igualdad y el x que aparece en el lado derecho son dos números diferentes. La fórmula toma entonces el siguiente aspecto:

Apliquemos iterativamente la fórmula. La primera pregunta es: ¿con qué valor inicial x₀ comenzamos? Para esto, echamos un vistazo a una gráfica del polinomio f(x). No es necesario que sea una gráfica muy precisa, solo tenemos que trazarla a grandes rasgos para ubicar las raíces aproximadas, que podemos ver que son tres (hay una raíz positiva, y dos raíces negativas):

Podemos ver de la gráfica que hay tres raíces para las cuales el polinomio es igual a cero. Una de las raíces está cercana al valor x.=.0.5 Si usamos dicho valor como valor inicial, después de varios pasos iterativos llevados a cabo con una calculadora ordinaria de bolsillo se va obteniendo lo siguiente:

Así pues, una raíz del polinomio está justo en -0.34729635. Como ya se indicó, el polinomio cúbico tiene tres raíces reales. Sin embargo, la fórmula iterativa obtenida no sirve para obtener las otras dos raíces del polinomio. Pero es posible obtener otra fórmula iterativa distinta que nos puede proporcionar esas otras dos raíces a partir de un estimativo cercano de las mismas:

La fórmula iterativa correspondiente será entonces:

La anterior fórmula iterativa se puede interpretar como dos fórmulas iterativas distintas:

Si usamos la fórmula iterativa con la raíz positiva y partimos con la estimación inicial x₀.=.2, vamos obteniendo lo siguiente:

Así pues, otra raíz del polinomio está justo en 1.87938524.

De las gráficas podemos ver que la tercera raíz está entre -1.0 y -2.0. Usando este valor como estimativo inicial y recurriendo a la fórmula iterativa con la raíz negativa, vamos obteniendo lo siguiente:

De este modo, la tercera raíz del polinomio está justo en -1.53208886.

¿Por qué funcionan estos procedimientos iterativos? Esto se puede apreciar de manera muy intuitiva superimponiendo en una misma gráfica los dos lados de una fórmula iterativa. En efecto, la fórmula usada para el procedimiento iterativo:

puede ser considerada como dos relaciones independientes para x:

Si trazamos en una misma gráfica ambas expresiones, los puntos en los cuales se intersectan las gráficas de cada fórmula corresponden a los ceros del polinomio original que estamos buscando:

De hecho, puede verse en la gráfica que hay otros dos puntos (además del punto resaltado con el texto “raíz”) en los cuales la línea recta de color azul intersecta con las curvas que representan al polinomio bajo análisis. Los otros dos puntos de intersección son, desde luego, las otras dos raíces.

PROBLEMA: Con la ayuda de una calculadora ordinaria de bolsillo, obténgase por lo menos una raíz que resuelva el siguiente polinomio:

De la ecuación proporcionada, podemos obtener sin mayores dificultades el siguiente algoritmo:

Empleando este algoritmo, y usando como punto de partida el valor x₀.=.0, en una calculadora ordinaria se puede llegar a lo siguiente:

x₅.=.x₆.=.-0.1445843

PROBLEMA: Con la ayuda de una calculadora ordinaria de bolsillo, obténgase por lo menos una raíz que resuelva el siguiente polinomio:

De la ecuación proporcionada, podemos efectuar el siguiente desarrollo para obtener el algoritmo deseado:

Empleando este algoritmo, y usando como punto de partida el valor x₀.=.5, en una calculadora ordinaria se puede llegar a lo siguiente:

x₄.=.x₅.=.5.0775742

PROBLEMA: Con la ayuda de una calculadora ordinaria de bolsillo, obténgase por lo menos una raíz que resuelva el siguiente polinomio:

De la ecuación proporcionada, podemos obtener sin mayores dificultades el siguiente algoritmo:

Empleando este algoritmo, y usando como punto de partida el valor x₀.=.0, en una calculadora ordinaria se puede llegar a lo siguiente:

x₄.=.x₅.=.-0.3319837

Se había mencionado arriba que si bien la extracción de la raíz cuadrada de un número puede resultar trivial en estos tiempos en los que se puede obtener una calculadora de bolsillo de bajo costo que tenga una tecla para la extracción de raíces cuadradas, si se quiere obtener la raíz cúbica de un número la cosa cambia por completo porque las calculadoras de bolsillo por regla general no incluyen una tecla para la extracción de raíces cúbicas. ¿Qué hacer en tales casos? ¿Podrá existir algún algoritmo que permita la extracción de raíces cúbicas con la ayuda de una simple calculadora de bolsillo? Resulta que la respuesta a esta pregunta es afirmativa, ya que no solo existe un algoritmo para la extracción de la raíz cúbica de cualquier número, sino inclusive el mismo algoritmo puede usarse para la extracción de otro tipo de raíces tales como raíces quíntuples, séxtuples, séptuples, etcétera. La prescripción algorítmica que se dará a continuación y la cual aceptaremos por lo pronto como un postulado matemático es la siguiente:

en donde n es el orden de la raíz que le queremos extraer al número y, x_i es un estimativo de dicha raíz y  x_i+1 es un estimativo más cercano aún a la raíz que queremos obtener.

Dado el algoritmo anterior, nuestro interés ahora es someterlo a pruebas para comprobar si realmente es cierto que funciona como se afirma, al igual que cuando compramos un carro deportivo de alta velocidad y queremos probarlo para ver si realmente es tan bueno como es promocionado. Para la extracción de raíces cúbicas, en el algoritmo se debe poner n.=.3 para así obtener la siguiente prescripción:

Con este algoritmo en nuestras manos, intentaremos extraer la raíz cúbica del número y.=.281 usando como estimativo inicial x_i.=.6.0. No requerimos más que una calculadora de bolsillo ordinaria para ir obteniendo y acumulando los resultados que se muestran a continuación en una forma parecida a como se hizo arriba:

De este modo, la raíz cúbica de 281 viene siendo 6.54991162.

PROBLEMA: Obténgase, con la ayuda de una calculadora ordinaria de bolsillo, las raíces cúbicas de los siguientes números:

 67.546       239478       5167023 

Compruébese asimismo en cada caso, dentro de la precisión numérica de la calculadora, que la respuesta obtenida en cada caso es la correcta.

Usando el algoritmo obtenido arriba, podemos obtener en pocos pasos los siguientes resultados:

Si el algortimo funciona para la obtención de raíces de orden n de cualquier número, el lector posiblemente ya haya caído en la cuenta de que debería funcionar también para n.=.2, o sea para la extracción de raíces cuadradas. De ser cierto, esto nos daría otro algoritmo diferente, además de los que ya se han dado arriba, para la extracción de raíces cuadradas.

Para n.=.2, o sea la extracción de raíces cuadradas, la prescripción general toma el siguiente aspecto (haremos un ligero cambio de notación usando la letra r para denotar a la raíz que se quiere obtener, en este caso una raíz cuadrada):

Usemos este procedimiento algorítmico para obtener la raíz cuadrada del número 67.89, o sea el mismo número de prueba que usamos arriba, pero resolviendo el asunto con el proceso iterativo que acabamos de obtener. Si recurrimos a este algoritmo para obtener la raíz cuadrada de y.=.67.89 y tomamos como punto de partida una estimación inicial r₀.=.8, entonces podemos ir obteniendo y acumulando los resultados que se muestran a continuación en una forma parecida a como se ha estado haciendo arriba:

¡Bastaron tan solo tres pasos para obtener con este algoritmo lo mismo que lo que se obtuvo arriba y que nos tomó casi el doble de tiempo! Indudablemente, hay algunas “recetas de cocina” que son más eficientes que otras, y es la tarea del matemático el mantenerse actualizado para estar siempre al tanto de los algoritmos más eficientes que se puedan encontrar (y hay la sospecha generalizada de que en este campo quedan todavía cosas por descubrir).

¿Cuántos algoritmos más diferentes a lo que ya hemos visto aquí cree el lector que puedan existir para la extracción de raíces cuadradas? ¿Cuál de todos ellos será el más eficiente?

Debe quedar claro a estas alturas que no hay un solo algoritmo para extraer raíces cuadradas, puede haber varios (el más sencillo es el del “tanteo” que consiste en elevar al cuadrado un número cuyo cuadrado esté cercano al número al que se le quiere sacar raíz cuadrada, y a continuación irle aumentando o dismimuyendo cada cifra que se le vaya agregando de forma tal que se vaya obteniendo una aproximación a la respuesta correcta, éste método es el que cualquiera puede llevar a cabo con una calculadora). Lo que más nos importa aquí es que todos los algoritmos que puedan ser concebidos para extraerle la raíz cuadrada a un número se pueden codificar como instrucciones precisas para que las lleve a cabo una computadora (en el caso del método del “tanteo” el procesador hace uso intensivo de operaciones elementales de multiplicación y comparación).

Vista la efectividad de la fórmula iterativa para obtener no solo la raíz cuadrada y la raíz cúbica sino la raíz n de cualquier número, la única interrogante que puede quedar aquí, estimulada por la curiosidad del lector, es: ¿de dónde salió esa fórmula?

La metodología científica exige no confiar en recetas ni en fórmulas mágicas que -aunque produzcan los resultados deseados- se desconozca el engranaje interno que las hace funcionar, porque ante una situación así no se está en una mejor posición que el nigromante que recitando de un viejo libro grueso y polvoriento en un lenguaje que le es desconocido trata de invocar a los muertos para adivinar el futuro, o el alquimista que logra obtener reacciones químicas interesantes o inclusive impresionantes sin tener la menor idea de lo que está haciendo y lo que está sucediendo. Se puede comprender la curiosidad que pueda tener un programador profesional por saber el origen de las recetas numéricas que se le proporcionan para resolver algún problema (por ejemplo, la aplicación del algoritmo Simplex para problemas de optimización linear), y en muchos casos podrá lograrlo si cuenta con estudios tanto en computación como en áreas especializadas de las matemáticas, en especial del Análisis Numérico. Sin embargo, el aumento exponencial del saber humano debido en buena medida a la especialización en las áreas científicas hace cada vez más difícil que un solo ser humano pueda ser bueno en todo y pueda saberlo todo, y habrá ocasiones en las que el programador tendrá que conformarse con la garantía de que las recetas algorítmicas que se le dan siempre harán el trabajo deseado cuando se mantengan dentro de los límites estipulados por los creadores de tales recetas.

De cualquier modo, por completitud y para no dejar dudas, a continuación se dará una derivación del proceso algorítmico usado para obtener la raíz n de cualquier número.

Sea x una aproximación a la raíz n del número y, de modo tal que hay algún error pequeño δ para el cual:

o lo que es lo mismo:

Siguiendo una línea de razonamiento que nos fue legada por Sir Isaac Newton, el lado izquierdo de lo anterior puede ser expandido con la ayuda del teorema del binomio:

Obsérvese en el lado derecho de esta relación que todos los sumandos después de los primeros dos términos son múltiplos de δ². Pero hemos partido del supuesto de que δ es un error pequeño, de modo tal que δ² será algo mucho más pequeño aún al grado de poder ser considerado insignificante, de modo tal que si despreciamos los sumandos que están multiplicados por potencias de  δ² o de orden mayor no se cometerá una equivocación significativa. Esto nos permite llevar a cabo el siguiente desarrollo (en el desarrollo, al aplicar la aproximación indicada, puesto que estrictamente hablando no se está hablando ya de una igualdad matemática sino de una aproximación se empleará el símbolo de aproximación ≈ en donde su uso es adecuado):

En la última expresión, el valor aproximado para x+δ debe ser una mejor estimación para el valor de la raíz n del número y que x, la aproximación original con la cual habíamos empezado. Esto implica que podemos tomar lo que se tiene del lado derecho como  x_i+1 , y así escribir:

que es la fórmula algorítmica general para la extracción de la raíz n de un número y que se había asentado arriba como postulado.

Si el lector supone que las calculadoras científicas de bolsillo están repletas de algoritmos para la evaluación de funciones matemáticas especializadas, no estará tan errado, ya que tratar de guardar (por ejemplo) en una gran tabla todas las respuestas posibles de todas las raíces cuadradas para cualquier número que pueda ser introducido en la calculadora a través del teclado es algo que excede con creces inclusive las capacidades de las computadoras de escritorio en los inicios del tercer milenio.

Todas las calculadoras científicas de bolsillo recurren a algoritmos para la evaluación de sus funciones matemáticas especializadas, por ejemplo la obtención del logaritmo de un número con una precisión de ocho o diez cifras significativas. Los algorimos que emplean deben ser sumamente eficientes y rápidos para darle una respuesta al usuario de una manera casi instantánea, de lo contrario puede haber una dilación de varios segundos (o incluso de varios minutos) en la obtención de una respuesta, una dilación comercialmente inaceptable. La única diferencia entre una calculadora científica de bolsillo y una calculadora ordinaria que solo puede efectuar operaciones aritméticas elementales son los algoritmos que tiene la primera grabados permanentemente en una memoria ROM, y siendo así entonces con un manual ijmpreso que contenga los algoritmos a ser usados para la evaluación de funciones matemáticas especializadas cualquier calculadora barata puede ser empleada para obtener las evaluaciones de cosas tales como logaritmos naturales, funciones trigonométricas, etcétera. En tal caso, la inversión en una calculadora científica sería más bien una cuestión de comodidad y conveniencia para no tener que llevar a cabo manualmente los procesos iterativos en los cuales se puede incurrir en alguna equivocación intermedia involuntaria que puede dar al traste con el resultado final, o sea la misma razón que dió origen a las computadoras. Obviamente, las empresas dedicadas a la producción y venta de calculadoras científicas no comparten con nadie sus algoritmos, manteniéndolos como secreto industrial, ya que suponen (y quizá tengan algo de razón) que la diseminación de tal información puede resultar en una pérdida potencial de clientela (de cualquier modo, cualquier matemático que esté al día les conoce de sobra sus trucos, aunque él mismo no querrá estar recurriendo a un manual de algoritmos para la evaluación de funciones matemáticas que la máquina pueda llevar a cabo mediante la opresión de una sola tecla).

Los ejemplos que se han presentado no han tomado en cuenta otro tipo de situaciones anómalas que se dar. Una de tales situaciones anómalas es aquella en la cual conforme la computadora se va aproximando a lo que parece ser una solución el proceso iterativo estalla en oscilaciones violentas que lejos de acercar a la computadora a la respuesta correcta la sumergen en ....

La computación científica no es el único lugar en donde recurrimos a algoritmos. Existen muchos otros ejemplos. Uno de ellos consiste en reordenar, alfabéticamente, varias hileras de texto que aparecen en forma desordenada (en literatura técnica inglesa, esta operación es conocida como sort). Supóngase que empezamos con la siguiente lista:

rueda
pantalla
avestruz
gato
carro
libro
serpiente
motocicleta
hotel
mosca

A primera vista, parecería que solo hay una manera posible de llevar a cabo el reordenamiento, empezando con las dos primeras palabras y reordenándolas alfabéticamente, y tras esto hacer lo mismo con la tercera palabra subiéndola “hasta arriba” cuanto sea necesario para que con ello las primeras tres palabras queden reordenadas alfabéticamente, continuando con el procedimiento hasta que se hayan agotado todas las palabras. De este modo, iremos recurriendo a los siguientes reordenamientos parciales.

pantalla
rueda
avestruz
gato
carro
libro
serpiente
motocicleta
hotel
mosca

seguido de:

pantalla
avestruz
rueda
gato
carro
libro
serpiente
motocicleta
hotel
mosca

seguido de:

avestruz
pantalla
rueda
gato
carro
libro
serpiente
motocicleta
hotel
mosca

y así sucesivamente, hasta llegar a la lista final ya puesta en orden alfabético después de varios pases:

avestruz
carro
gato
hotel
libro
mosca
motocicleta
pantalla
rueda
serpiente

Sin embargo, el reordenamiento mostrado no es la única manera posible de llevar a cabo el reordenamiento alfabético que se mostró arriba. Otra manera posible consiste en subdividir la lista original partiéndola en dos mitades, reordenando las palabras en la primera mitad y reordenando las palabras en la segunda mitad, y tras esto ir insertando cada palabra de la segunda mitad en el lugar que le corresponda en la primera mitad. De este modo, la lista original particionada a la mitad:

rueda
pantalla
avestruz
gato
carro

libro
serpiente
motocicleta
hotel
mosca

viene quedando de la siguiente manera con cada mitad reordenada:

avestruz
carro
gato
pantalla
rueda

libro
serpiente
motocicleta
hotel
mosca

Tras esto, podemos ir metiendo cada palabra de la segunda lista en el lugar que le corresponda en la primera lista para llegar así al reordenamiento total de la lista original. Pero la pregunta importante vendría siendo: ¿Es esta manera de lograr las cosas una manera más efectiva que la que fue dada anteriormente? Ya vimos en la obtención de algoritmos para la extracción de la raíz cuadrada de un número que no todos los algoritmos son iguales, aunque produzcan los mismos resultados y a primera vista el segundo procedimiento de reordenamiento que se ha dado aquí no parece ser mejor que el anterior, y cabe observar además que elaborar un programa computacional para este segundo algoritmo será sin duda alguna algo más complejo y sofisticado.

Además de las dos posibilidades mostradas arriba, hay otro tipo de reordenamiento conocido en la literatura técnica como un reordenamiento burbuja (bubble sort), y se puede llevar a cabo con números (en lugar de letras o palabras) siguiendo una secuencia numérica. Supóngase por ejemplo que se quiere ordenar la siguiente lista de números:

54   26   93   17   77   31   44   55   20

poniendo el número más bajo en el extremo izquierdo y poniendo el resto en orden ascendente hasta que el mayor de todos (93) se encuentre en el extremo derecho. Tras un primer pase con el procedimiento que se ha dado recorriendo la lista completa de izquierda a derecha se tiene lo siguiente:

26   54   17   77   31   44   55   20 93

obtenido en forma más explícita de la siguiente manera:

El resultado final mostrado en el extremo inferior es el resultado del primer recorrido completo a lo largo de la lista, siendo obvio que se requerirá de recorridos adicionales para poder obtener un reordenamiento completo.

PROBLEMA: Escríbase una subrutina en lenguaje BASIC para llevar a cabo el reordenamiento de una lista de N números mediante el algoritmo de reordenamiento burbuja. Póngase a prueba dicho procedimiento procurando alguna versión del lenguaje BASIC y usando la lista de números dada arriba.

Una implementación posible del algoritmo de reordenamiento burbuja es la siguiente (el valor de N tiene que ser especificado antes de usar la subrutina):

1000  REM SUBRUTINA ALGORITMO REORDENAMIENTO BURBUJA
1010  REM DE UNA LISTA DE N NUMEROS
1020  TRUEQUE = 0
1030  FOR I = 1 TO N-1
1040    IF A(I) > A(I+1) THEN TRUEQUE = 1
1050    TEMP = A(I) : A(I) = A(I+1) : A(I+1) = TEMP
1060  NEXT I
1070  IF TRUEQUE = 1 THEN 1020
1080  REM REORDENAMIENTO BURBUJA COMPLETADO
1090  RETURN

La subrutina BASIC supone que los N números a ser reordenados están puestos previamente en un arreglo A. Una variable TRUEQUE es usada para especificar si ocurre un intercambio durante un pase (TRUEQUE=1). Si no ocurre ningún intercambio (TRUEQUE=0) entonces entonces el reordenamiento burbuja de la lista está completado. El bucle FOR en los números 1030 y 1060 es llevado a cabo N-1 veces. En la línea 1050 con la ayuda del colon (:) se han puesto en una misma línea lo que de otro modo ocuparía tres líneas distintas. Más aún, los enunciados que siguen a la prueba comparativa entre A(I) y A(I+1) serán ejecutados solo si A(I) es mayor que A(I+1). En caso contrario, la línea 1060 es ejecutada.

Hay disponibles en Internet algunos interpretadores BASIC un poco más sofisticados que permiten escribir el programa anterior usando una sintaxis que proporciona una capacidad para programación en bloques similar a la que se encuentra en enunciados del lenguaje Pascal, lo cual hace que el programa sea más legible y que se requieran menos enunciados que cuando la capacidad para la programación estructurada en bloques está ausente, como lo muestra la siguiente versión en un BASIC estructurado:

IF A(I) > A(I-1) THEN
   BEGIN
      TRUEQUE = 1 ;
      TEMP = A(I) ;
      A(I) = A(I+1) ;
      A(I+1) = TEMP ;
   END ;

Con el reordenamiento burbuja si la lista está completamente desordenada se requiere un total de:

intercambios. El reordenamiento burbuja es uno de los algoritmos de reordenamiento menos eficientes que hay, habiendo otros tales como el reordenamiento concha (shell sorting).

PROBLEMA: Escríbase una subrutina en lenguaje BASIC para llevar a cabo el reordenamiento de una lista de N hileras de texto mediante el algoritmo de reordenamiento burbuja. Póngase a prueba dicho procedimiento procurando alguna versión del lenguaje BASIC y usando algunas cuantas palabras como hileras de texto.

El procedimiento a seguir aquí es casi idéntico, con cambios mínimos que reflejan el hecho de que los artículos a ser reordenados son hileras de texto en lugar de números:

1000  REM SUBRUTINA ALGORITMO REORDENAMIENTO BURBUJA
1010  REM DE UNA LISTA DE N HILERAS
1020  TRUEQUE = 0
1030  FOR I = 1 TO N-1
1040    IF A$(I) > A$(I+1) THEN TRUEQUE = 1
1050    TEMP$ = A$(I) : A$(I) = A$(I+1) : A$(I+1) = TEMP$
1060  NEXT I
1070  IF TRUEQUE = 1 THEN 1020
1080  REM REORDENAMIENTO BURBUJA COMPLETADO
1090  RETURN

Una cosa a tener presente es que al ser presentada una lista a ser puesta en cierto orden, se sobreentiende que, exceptuando los datos situados en los extremos de la lista, cada dato va precedido por un dato inmediato y por otro dato que le sigue también en forma inmediata. Esto implica necesariamente que a cada dato se le debe agregar por lo menos otro número, un número que apunte hacia la localidad de la memoria en donde se encuentre el dato que le sigue en forma inmediata. Esto es inevitable, porque si suponemos que los datos de la lista estarán ubicados en localidades contiguas de la memoria RAM, supondremos mal, ya que cada dato puede estar situado en cualquier parte de la memoria RAM. Lo ideal sería desde luego que en el caso de los datos “avestruz”,  “carro”,  “gato” y “hotel”, el primer dato “avestruz” estuviera en situado empezando en la localidad de la memoria 3465, el siguiente dato “carro” estuviera situado empezando en la localidad de la memoria 3473, el siguiente dato  “gato” estuviera situado empezando en la localidad de la memoria 3477, y el dato  “hotel” estuviera situado empezando en la localidad de la memoria 3482. Aún comenzando con una lista ya ordenada, conforme se van borrando datos de la lista y se van agregando otros datos nuevos que tienen que ser puestos en otras localidades de la memoria RAM al no “caber” en el lugar en donde fue borrado un dato anterior (tómese en cuenta que cada palabra tiene una cantidad de letras variable) se van creando “hoyos” y los datos se van desparramando por doquier, de modo tal que el primer dato “avestruz” puede terminar situado empezando en la localidad de la memoria 4651, el siguiente dato “carro” puede terminar situado empezando en la localidad de la memoria 5832, el siguiente dato  “gato” tal vez ya haya sido borrado de la lista, y el dato  “hotel” puede terminar situado empezando en la localidad de la memoria 9341. La única manera en la cual la lista pueda seguir existiendo como tal es considerando dicha lista como una lista enlazada, con los datos encadenados entre sí como ocurre con los eslabones de una cadena, y esto solo se puede lograr anexando a cada dato un número que apunte directamente hacia la localidad de la memoria RAM en donde se encuentra el dato que le sigue, de forma tal que los datos permanezcan concatenados. De este modo, al irse borrando e irse agregando nuevos datos a la lista los números anexados a cada dato son actualizados según se requiera para que siempre apunten hacia la localidad en la cual se encuentra el dato inmediato siguiente. Estos números que apuntan hacia el siguiente dato son precisamente los punteros o apuntadores, y forman parte inevitable de lo que tiene que ser agregado a cada dato para que una lista pueda existir como tal dentro de una base de datos de una computadora, por lo que este equipaje adicional no puede considerarse como un mal necesario. Este es precisamente el origen de los punteros o apuntadores que vemos en muchos lenguajes de alto nivel, son parte necesaria e integral de cada lenguaje para poder manejar listas de arreglos (conocidas en literatura técnica inglesa como arrays).

Los algoritmos mostrados dados arriba para el reordenamiento alfabético de las palabras o los números de una lista no son los únicos, y es posible que el lector se sienta tentado a inventar en estos momentos el suyo propio. Hay muchos otros algoritmos para llevar a cabo el reordenamientos de los elementos que hay en una lista, tantos que se requiere de una área de estudio dedicada exclusivamente a dicho tema para tomar conocimientos someros acerca de los algoritmos de reordenamiento más utilizados así como sus ventajas y desventajas relativas. Apenas hemos tocado la superficie. El texto clásico de referencia para este tema es el libro The Art of Computer Programming, Volume 3: Sorting and Searching de Donald E. Knuth.

Otro campo en el cual se hace uso de algoritmos es aquél en el cual se lleva a cabo una búsqueda entre lo que parece ser un mar interminable de datos. La empresa Google ha hecho de esto su especialidad y con ello ha logrado construír un vasto imperio informático. Para un ejemplo de ello, considérese un diccionario o una enciclopedia que consta de cinco mil entradas; supóngase además que queremos encontrar información relacionada con cierta palabra. Si la búsqueda se lleva a cabo con la ayuda de una máquina siguiendo siempre un estricto orden alfabético ascendente (de la A hasta la Z), y si la palabra es algo como “árbol”, entonces estamos con suerte porque seguramente se dará con dicha palabra después de haber recorrido a lo sumo unos cuantos cientos de palabras. Pero si la palabra es algo como “zoológico”, entonces para algo que se encuentra cerca del final de la lista tendremos que recorrer casi las cinco mil entradas o veinte mil entradas que hay en el diccionario o en la enciclopedia para dar con ella. Este método de búsqueda no parece ser el más efectivo, y de hecho hay otro conocido como la búsqueda binaria. En este método, partimos la lista de cinco mil entradas en dos mitades; si la palabra buscada no se encuentra en la primera mitad seguramente se encuentra en la segunda mitad, y no requiere mucho tiempo ni cálculo computacional para llegar a esta conclusión. Si la palabra buscada se encuentra en la segunda mitad, repetimos el procedimiento dividiendo dicha mitad en dos mitades, y la palabra se debe encontrar en una de dichas mitades. Continuando el proceso de subdivisión en mitades, se puede demostrar que no importando la palabra de que se trate podemos en promedio llegar a ella de una manera mucho más rápida que ateniéndonos siempre a una búsqueda por orden alfabético ascendente estricto. Además de la búsqueda binaria, hay otros tipos de búsqueda en los que no entraremos aquí en mayor detalle, aunque el lector tal vez sospeche ya que se puede conceptualizar un procedimiento refinado de búsqueda que use no una sola técnica sino una combinación optimizada de dos o más técnicas.

La importancia de contar con un algoritmo para la solución del problema computacional que sea es que cuando se tiene a la mano el algoritmo la elaboración del programa computacional computacional en el lenguaje que sea está prácticamente dada. Considérese un problema de minimización de cierta función matemática multi-variables en el cual queremos obtener el valor mínimo de dicha función así como la combinación del valor de los argumentos que producen tal mínimo. Si hay varias maneras de solucionar el problema, le corresponde a un matemático escoger el método que prefiere usar sobre los demás métodos, y supondremos que su criterio estará guiado por una buena educación académica. Una vez que el algoritmo ha sido seleccionado, el matemático se lo proporcionará al programador en una serie de pasos. El programador a su vez decidirá si quiere programar el algoritmo usando el lenguaje BASIC, el lenguaje Pascal, el lenguaje FORTRAN, el lenguaje PL/1, o cualquier otro lenguaje que considere que mejor se presta para la implementación del algoritmo.