Una máquina de estados finitos no es más que una combinación de lógica secuencial y lógica combinatórica, así se construye, usando compuertas lógicas (AND, OR, NOT) y flip-flops. Quizá la máquina de estados finitos más sencilla es aquella que consta de una sola entrada, pudiendo tomar uno de varios estados en cada “pulso de reloj” dependiendo del símbolo de entrada (un “uno” o un “cero”) que le esté siendo aplicado en ese momento:
La terminal usada para aplicar los pulsos de reloj no es considerada como una entrada, es simplemente el medio para llevar a la máquina de estados finitos de un estado a otro, siendo por lo tanto una máquina secuencial (como la máquina Turing) cien por ciento determinista (para cierta entrada y cierto estado actual, el estado siguiente está ya prefijado). A diferencia de máquinas secuenciales tales como un contador binario de conteo ascendente construído con dos flip-flops J-K y que por lo tanto tendrá cuatro estados diferentes (siendo el primer estado s0 igual a “00”, siendo el segundo estado s1 igual a “10”, siendo el tercer estado s2 igual a “01” y siendo el cuarto estado s3 igual a “11”) pasando de un estado al siguiente en cada pulso de reloj sin recibir entrada externa alguna, la máquina de estados finitos de la que estamos hablando recibe por lo menos una entrada del exterior, y el estado que tomará al recibir un pulso de reloj dependerá no solo del estado actual en que se encuentre sino del valor de la entrada externa que le está siendo aplicada.
La forma pictórica convencional de representar el comportamiento de una máquina de estados finitos es mediante un grafo dirigido conocido comunmente como un grafo de estado, de lo cual se presenta el siguiente ejemplo:
La lectura de un grafo de estado es algo relativamente sencillo. Suponiendo que se parte con la máquina en el estado inicial s0, y se aplica una entrada de “1”, entonces de acuerdo a la flecha curva se seguirá en el mismo estado al recibir la máquina un pulso de reloj, lo cual significa que la primera parte de la hilera puede constar de cualquier número de “unos”, ya sea 11, 11111 ó 11111111, lo cual se representa como 1* en el lenguaje matemático de las expresiones regulares. Al aplicar una entrada de “0”, la máquina pasa directamente del estado s0 al estado s1 con el siguiente pulso de reloj. Hasta aquí, se ha reconocido la hilera 1*0. Una vez en el estado s1, si se aplica un “0” entonces la máquina pasará del estado s0 al estado final de aceptación s2 al recibirse un pulso de reloj. Se acostumbra destacar los estados finales con un doble círculo. Hasta aquí se ha reconocido la hilera 1*00. Y si estando en el estado final de aceptación se sigue aplicando repetidamente una entrada de “0” entonces los subsecuentes pulsos de reloj dejarán a la máquina en el mismo estado final de aceptación. De este modo, la máquina que corresponde al grafo puede reconocer las hileras que formen parte del conjunto de expresiones regulares 1*000*. Obsérvese que hay otras entradas que desvían a la máquina hacia el estado s3, el cual no es un estado final.
A continuación se presenta un gráfico animado que nos muestra los cambios que va experimentando una máquina de estados finitos que reconozca el conjunto de expresiones regulares 1*000* al serle presentada la hilera 11100000 que forma parte de dicho conjunto, suponiendo que la máquina de estados finitos fue construída usando flip-flops J-K que cambian de estado al ir la terminal de entrada de los pulsos de reloj de “1” (representada con un circulito de color rojo que denota “encendido”) a “0” (representada con un circulito sin color interno denotando con ello “apagado”):
Este es el comportamiento de la misma máquina descrita por el grafo de estado que fué dado arriba. Obsérvese que no hay modo alguno de que, en caso de que la máquina con una entrada posterior de “1” sea sacada del estado final de aceptación s2 para ser enviada hacia el estado s3, la máquina pueda salir del estado s3 para poder regresar al estado final de aceptación s2.
Una forma alterna de representar un grafo de estado prescindiendo del doble círculo que indica un estado final de aceptación de “1” es anexando a cada estado el valor de la salida de la máquina separándolo (dentro del círculo que representa a un estado) con una diagonal “/”, de modo tal que -dentro de un círculo- el símbolo “s2/0” indica que la máquina se encuentra en el estado s2 y al encontrarse en tal estado su salida es igual a “0”. Usando esta notación, el grafo que hemos visto arriba toma el siguiente aspecto:
La máquina que se acaba de describir es mejor conocida como una máquina Moore, una máquina para la cual su salida (o salidas) depende tanto del estado actual en el que se encuentra la máquina así como de la entrada (o las entradas) que se le esté aplicando a la máquina al momento de ocurrir la transición, enfatizándose el hecho de que la entrada (o entradas) influye únicamente en determinar el estado siguiente de la máquina a partir de cierto estado, la entrada no es combinada en modo alguno con la salida de la máquina cuando la máquina ha cambiado de estado. Un paradigma de estas máquinas el registro de transferencia (también conocido como registro de corrimiento o registro de desplazamiento), el cual tiene por lo menos una entrada (en el caso de un registro de transferencia con entrada serial y salida serial) y en el cual el estado posterior del registro depende no solo del estado previo del registro sino también de la entrada (o las entradas) aplicadas al registro al momento de llevarse a cabo la transición de un estado a otro. El registro de transferencia más genérico que incluye todas las posibilidades (entrada serial, entrada paralela, salida serial, salida paralela) es el siguiente:
Si se trata de un registro de transferencia serial construído con cinco flip-flops tipo D y el estado inicial de la máquina Q0Q1Q2Q3 es tomado como 00000, entonces poniendo un “1” en la terminal de entrada serial (por el lado izquierdo en la figura de arriba) el siguiente estado de la máquina será 10000, mientras que poniendo un “0” el siguiente estado de la máquina será 00000 (se mantiene igual).
Hay otro tipo de máquina más compleja. Se trata de la máquina Mealy, en la cual las entradas condicionantes (con lógica combinatórica propia del diseño) que posee la máquina no sólo determinan el siguiente estado de la máquina, sino que las entradas también se combinan de alguna manera con el estado de la máquina para producir una salida combinada resultante. Podemos bosquejar la relación que hay entre una máquina Moore y una máquina Mealy del modo siguiente:
La máquina Mealy introduce un grado adicional de dificultad en los diseños, ya que si la salida de la máquina depende no sólo del estado previo de la máquina sino también del valor de lo que se le esté aplicando en la(s) terminal(es) de entrada, entonces tales entradas tienen que estar sincronizadas y a la par con la aplicación de los pulsos de reloj que mueven a la máquina de un estado a otro.
Existen disponibles en Internet varios programas de simulación que ayudan en la construcción de los grafos de estado usados para la representación de las máquinas de estados finitos, conocidas de modo más formal como autómatas dentro de la Teoría de Autómatas. Uno de tales programas es JFLAP:
PROBLEMA: Escríbase la expresión regular que describe las hileras que puede reconocer la siguiente máquina de estados finitos:
La máquina puede reconocer cualquier hilera que forme parte del conjunto 1*0(00)*1, o sea hileras que comienzan con “1”, seguidas de un “0” y de pares “00” (incluído ninguno) terminando con un “1”.
El grafo de estado es quizá una manera más clara e intuitiva de presentar el comportamiento de una máquina de estados finitos que la tabla secuencial mejor conocida como tabla de estado:
| Siguiente estado | Salida | ||
| Entrada presente | |||
| Estado actual | 0 | 1 | |
| s0 | s1 | s0 | 1 |
| s1 | s4 | s3 | 1 |
| s2 | s0 | s5 | 0 |
| s3 | s4 | s1 | 1 |
| s4 | s5 | s5 | 0 |
| s5 | s3 | s0 | 1 |
En la tabla de estado anterior, la columna extrema derecha (con los datos destacados en fondo amarillo claro) no tiene nada que ver con las dos columnas intermedias de la tabla que proporcionan el siguiente estado de la máquina dependiendo de que la entrada actual a la máquina sea “uno” o “cero”, simplemente proporciona la salida que corresponde a cada estado que aparece en la columna extrema izquierda (con los estados destacados también en fondo amarillo), y para evitar confusiones tal vez resulte un poco más clara la siguiente tabla equivalente:
| Siguiente estado | ||
| Entrada presente | ||
| Estado actual | 0 | 1 |
| s0 /1 | s1 | s0 |
| s1 /1 | s4 | s3 |
| s2 /0 | s0 | s5 |
| s3 /1 | s4 | s1 |
| s4 /0 | s5 | s5 |
| s5 /1 | s3 | s0 |
Las máquinas de estados finitos que se han descrito arriba tienen como entradas sólo dos símbolos, “0” y “1” aplicados en un terminal de entrada. Pero podemos tener una máquina que tiene varias terminales de entrada,como la siguiente que tiene tres terminales de entrada:
En la máquina anterior, si podemos aplicar un “0” (apagado) ó un “1” (encendido) en cada una de las tres terminales, hay entonces ocho combinaciones posibles pudiendo asignar un símbolo diferente a cada combinación, lo cual permite que en vez de un alfabeto limitado {0,1} se pueda tener un alfabeto más amplio como {00,01,10,11} que en el caso de dos terminales de entrada podemos simbolizar como {a,b,c,d}. Una tabla secuencial con el alfabeto {a,b,c} es la siguiente:
| Siguiente estado | Salida | |||
| Entrada presente | ||||
| Estado actual | a | b | c | |
| s0 | s2 | s1 | s4 | 0 |
| s1 | s2 | s0 | s4 | 1 |
| s2 | s3 | s4 | s2 | 0 |
| s3 | s3 | s1 | s0 | 0 |
| s4 | s3 | s1 | s0 | 1 |
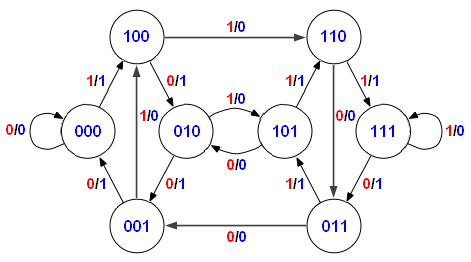
PROBLEMA: Suponiendo que la máquina cuyo grafo de estado es el siguiente:
tiene las siguientes salidas para cada estado:
s1/0 , s2/0 , s3/0 , s4/1
elabórese la tabla de estado que corresponde al grafo de estado.
La tabla de estado correspondiente al grafo proporcionado es la siguiente:
| Siguiente estado | Salida | ||||
| Entrada presente | |||||
| Estado actual | a | b | c | d | |
| s1 | s2 | 0 | |||
| s2 | s2 | s1 | s4 | 0 | |
| s3 | s1 | s4 | 0 | ||
| s4 | s3 | 1 | |||
Obsérvese que no solo no todos los estados son alcanzables a partir de cierto estado, sino que puede haber entradas que no producen efecto alguno en cada transición de estado, dejando a la máquina en el mismo estado en el que se encontraba antes. Esto significa que el comportamiento completo de la máquina debe poder ser descrito mediante el siguiente grafo de estado ampliado:
Con esto último, la tabla de estado, sin huecos, viene tomando el siguiente aspecto:
| Siguiente estado | Salida | ||||
| Entrada presente | |||||
| Estado actual | a | b | c | d | |
| s1 | s2 | s1 | s1 | s1 | 0 |
| s2 | s2 | s1 | s4 | s2 | 0 |
| s3 | s1 | s4 | s3 | s3 | 0 |
| s4 | s4 | s4 | s4 | s3 | 1 |
En una máquina con tres terminales de entrada, pudiendo tomar cada entrada un valor de “0” (apagado) ó un valor de “1” (encendido), empleando todas las combinaciones posibles a su máxima capacidad podemos tener un alfabeto de entrada más amplio como el siguiente:
{000,001,010,011,100,101,110,111} = {0,1,*,X,Y,Z,(,)}
Esto podría hacer sospechar que con una máquina de estados finitos podemos lograr lo mismo que lo que podemos lograr con una máquina Turing. Sin embargo, como veremos más abajo, esto no es posible.
Todos los grafos de estado y las tablas de estado que hemos visto arriba son grafos y tablas propias de las máquinas Moore. Dado cierto estado y cierta entrada, con ello el estado siguiente queda determinado en forma unívoca. Los grafos de estado para las máquinas Mealy son diferentes, como el siguiente:
La forma de leer este grafo de estado Mealy es la siguiente: Hay un círculo para cada estado y una flecha saliendo de cada estado para cada entrada. Cada flecha está etiquetada con el número (puesto en color rojo) que corresponde a la entrada, y la salida resultante (puesta en color azul). De este modo, podemos leer: “partiendo del estado s0, si se aplica una entrada igual a 1 la salida será 0 y la máquina pasará al estado s2”. Y también: “partiendo del estado s1, si se aplica una entrada igual a 1 la salida será 1 y la máquina pasará al estado s2”.
Igualmente, las tablas de estado para las máquinas Mealy son diferentes, ya que mientras que para las máquinas Moore las tablas de estado tienen el siguiente aspecto:
| Siguiente estado sn+1 |
Salida Z |
|||
| Entrada presente | ||||
| Estado actual | x1 | x2 | x3 | |
| s0 | s1 | s2 | s0 | 0 |
| s1 | s2 | s3 | s0 | 0 |
| s2 | s2 | s2 | s0 | 0 |
| s3 | s4 | s2 | s0 | 0 |
| s4 | s4 | s4 | s0 | 1 |
para las máquinas Mealy las tablas de estado se tiene algo como lo siguiente:
| Estado actual | x1 sn+1,Z |
x2 sn+1,Z |
x3 sn+1,Z |
| s0 | s1,0 | s2,0 | s0,0 |
| s1 | s2,0 | s3,0 | s0,0 |
| s2 | s2,0 | s2,0 | s0,0 |
| s3 | s2,1 | s2,0 | s0,0 |
Obsérvese que en la tabla de estado para la máquina Mealy ya no es posible asociar una salida en forma unívoca para cada estado en virtud de que la salida de la máquina depende no solo del estado nuevo de la máquina sino también de la entrada que está siendo aplicada. En efecto, el estado de la máquina y la salida de la máquina Mealy han dejado de ser sinónimos.
Con la finalidad de que la diferencia entre las máquinas Moore y las máquinas Mealy quede perfectamente clara, considérese un registro de transferencia de tres “bits” con entrada serial, el cual será construído con tres flip-flops D:
Suponiendo que este registro de transferencia se encuentre inicialmente en el estado 000, el grafo de estado de esta máquina Moore tendrá el siguiente aspecto:
PROBLEMA: Constrúyase la tabla de estado para la máquina Moore dada arriba.
La tabla pedida tendrá el siguiente aspecto:
| Siguiente estado sn+1 |
||
| Entrada presente | ||
| Estado actual | 0 | 1 |
| s1 = 000 | s1 | s2 |
| s2 = 100 | s4 | s6 |
| s3 = 001 | s1 | s2 |
| s4 = 010 | s3 | s5 |
| s5 = 101 | s4 | s6 |
| s6 = 110 | s7 | s8 |
| s7 = 011 | s3 | s5 |
| s8 = 111 | s7 | s8 |
Supóngase ahora que el registro de transferencia es modificado agregando algo de lógica combinatórica, agregando dos compuertas lógicas OR-exclusivo:
obteniendo así el siguiente circuito:
Obsérvese que una de las entradas del primer OR-exclusivo, destacada en color magenta, es tomada directamente de la entrada al circuito; y la salida del primer OR-exclusivo, que depende de la entrada, es enviada a la entrada del segundo OR-exclusivo, cuya salida que tomaremos como la salida del circuito dependerá por lo tanto también del “0” ó del “1” que haya a la entrada. Si el estado de esta máquina está dado por el estado de cada uno de los tres flip-flops D, y es Q1Q2Q3, obviamente el estado de la máquina (que es un número binario de tres bits) será diferente de la salida de la máquina (que es un número de 1 bit), y describir el comportamiento de la máquina requerirá un grafo como el siguiente:
Los números rojos en este grafo son los mismos que los que corresponden a los números de color café obscuro para el grafo del registro de transferencia de tres bits dado más arriba, y representan las entradas que llevan a la máquina al estado siguiente, mientras que los números de color azul representan la salida Z del circuito habiéndose procesado y agregado el efecto de cada entrada al circuito mediante los bloques OR-exclusivo.
PROBLEMA: Obténgase la tabla de estado para la máquina Mealy descrita por el grafo anterior.
| Siguiente estado y salida producida sn+1, Z |
||
| Entrada presente | ||
| Estado actual | 0 | 1 |
| s1 = 000 | s1,0 | s2,1 |
| s2 = 100 | s4,1 | s6,0 |
| s3 = 001 | s1,1 | s2,0 |
| s4 = 010 | s3,1 | s5,0 |
| s5 = 101 | s4,0 | s6,1 |
| s6 = 110 | s7,0 | s8,1 |
| s7 = 011 | s3,0 | s5,1 |
| s8 = 111 | s7,1 | s8,0 |
A modo de ejemplo de la construcción del grafo de estado para la máquina Mealy, supóngase que el estado de la máquina en cierto momento es:
s = Q1Q2Q3 = 010
Si ponemos un “1” en la entrada D1 del primer flip-flop D y aplicamos un pulso de reloj para llevar a la máquina de un estado a otro, entonces por la acción del registro de transferencia el siguiente estado de la máquina será 101. ¿Y cuál será la salida Z que se produce? Suponiendo que mantenemos el “1” sin removerlo de la entrada D1, entonces tomando en cuenta la acción del bloque OR-exclusivo para el cual la salida es “1” cuando ambas entradas son diferentes (“0” en una entrada, “1” en la otra), entonces rastreando la lógica combinatórica se tiene la siguiente situación:
pudiéndose ver que la salida será Z.=.1. En pocas palabras, con un “1” en la entrada la máquina produce un “1” en su salida Z al pasar la máquina del estado 010 al estado 101, siendo esto lo que se pone en la flecha que conduce del estado 010 al estado 101:
entrada que produce la transición/salida resultante = 1/1
Posiblemente aquí el lector se haya dado cuenta de una situación algo incómoda. Para que lo anterior funcione de la manera deseada tal y como se asienta tanto en el grafo de estado como en la tabla de estado, es requisito indispensable que el “bit” puesto a la entrada D1 del primer flip-flop sea puesto en dicha entrada justo en el momento preciso en el que ocurre la transición. Si el “bit” de entrada es puesto un poco antes, su efecto en la salida Z será reflejado en forma casi instantánea, y si es puesto un poco después de haber ocurrido la transición también el efecto se verá reflejado en forma casi instantánea. Considérese que una vez que la máquina ya se encuentra en el estado 101 después de la primera transición, se pone a su entrada un bit igual a “0” con la intención de llevar la máquina hacia el estado 010 con una segunda transición. Si el bit “0” se pone un poco antes de llevarse a cabo la segunda transición con la aplicación del pulso de reloj, entonces la salida del primer OR-exclusivo cambiará de “0” a “1” al ser una entrada igual a “0” y la otra entrada igual a “1”. Con esto, ambas entradas al segundo OR-exclusivo serán iguales (con un valor de “1”) y la salida Z del circuito cambiará de “1” a “0” antes de haberse llevado a cabo la transición. Y si el bit “0” se pone un poco después de llevarse a cabo la segunda transición, entonces no tendrá ningún efecto en el estado de la máquina, la cual permanecerá en su estado anterior en virtud de que las entradas a los flip-flops tienen que tener un valor fijo y preciso al momento de llevarse a cabo la transición (o antes) y no después. Idealmente, se requeriría que justo al momento de ocurrir una transición el bit a la entrada D1 ya tenga el valor que toca meter en el registro de transferencia, pero no antes, lo cual en la práctica es algo imposible de lograr. Este problema no ocurre en el registro de transferencia llano (máquina Moore, sin las dos compuertas OR-exclusivo), el cual es una máquina que produce un nivel de salida (supondremos que la salida del registro de transferencia será tomada como la salida Q3 del tercer flip-flop) que se mantiene constante hasta la aplicación del siguiente “pulso de reloj”, y es lo que podemos llamar una máquina que funciona como pulso de entrada-nivel de salida, ya que si la salida (o salidas) es una función de las variables de estado únicamente (el estado previo de la máquina) entonces la salida (o salidas) será un nivel cuyo valor estará definido en los intervalos de tiempo que ocurren entre los pulsos de entrada, en lugar de que esté definido al momento en que son aplicados los pulsos de entrada. En cambio, en la máquina Mealy que hemos visto arriba, si la salida (o salidas) van a ser funciones no sólo de las variables de estado sino también de la entrada (o las entradas) entonces la salida debe ser un pulso (y no un nivel) obtenido al combinar las variables de estado con la entrada, en cuyo caso podemos hablar de una máquina que funciona como pulso de entrada-pulso de salida, lo cual para que ocurra requiere de la adición de circuitos y compuertas adicionales de sincronización (no mostrados en la máquina Mealy de arriba) que eviten los imprevistos inevitables cuando se aplica una entrada (o entradas) no en el momento justo y preciso en el cual se lleva a cabo la transición de un estado a otro sino un poco antes o un poco después.
No entraremos aquí en mayores detalles sobre el tema de las máquinas Moore y las máquinas Mealy, porque ello es irrelevante para nuestros fines presentes. Nos limitaremos a seguir considerando la máquina de estados finitos como una máquina secuencial que estando en cierto estado pasa a un estado posterior dependiendo del estado previo y de la entrada que está siendo aplicada al momento de ocurrir la transición.
Para nuestros propósitos, no estamos considerando máquinas secuenciales autónomas que no cuentan con terminal de entrada alguna excepto la que se requiere para aplicar los “pulsos de reloj” que hacen que la máquina pase de un estado al siguiente. El paradigma de esto es el contador binario, el cual carece de entradas y el cual va pasando de un estado binario al siguiente al recibirse cada “pulso de reloj”. Si se trata de un contador binario ascendente construído con dos flip-flops J-K, y cada estado de la máquina representa una de las combinaciones {00,01,10,11}, entonces llamando al estado final de aceptación como el estado en el cual las salidas de ambos flip-flops son ambas “1”, sin necesidad de recurrir a esquemas elaborados de diseño la máquina secuencial de conteo se puede construír enviando ambas salidas a un bloque lógico AND de modo tal que se tenga para la máquina:
salida = Q1 · Q2
Esta máquina secuencial tendrá el siguiente aspecto:
El lector se deberá convencer que la salida correspondiente a lo que estamos llamando aquí el estado final de aceptación ocurre sólo cuando tanto ambas salidas Q1 y Q2 de los dos flip-flops J-K son “1”. La característica principal de este tipo de máquinas secuenciales es que no se puede construír para ellas ninguna tabla de estado porque carecen de entradas, y el grafo de estado es una sucesión lineal encadenada de un estado a otro, y por lo tanto este tipo de máquinas secuenciales autónomas son incapaces de poder reconocer ninguna hilera de símbolos.
Volviendo al tema de las expresiones regulares, es un hecho incontrovertible que cualquier expresión regular puede ser reconocida por una máquina de estados finitos, dada una expresión regular siempre podemos diseñar una máquina de estados finitos que reconozca esa expresión regular. Esto es conocido como el teorema de Kleene, y fue descubierto por el matemático Stephen Kleene en 1956. Expresado en su forma más general, el teorema nos dice lo siguiente:
Teorema de Kleene: Cualquier conjunto de hileras que pueda ser reconocido por una máquina de estados finitos es un conjunto regular, y en forma conversa, cualquier conjunto regular puede ser reconocido por alguna máquina de estados finitos.El primer gran inconveniente de una máquina de estados finitos es que una vez diseñada y construída sólo sirve para un propósito, como el reconocer la expresión regular 0*101*(10)*. Si se desea tener una máquina de estados finitos que reconozca otra expresión regular como (01)*110*1(100)*, hay que empezar desde el principio construyendo otra máquina, desbaratando quizá la máquina anterior para reciclar los componentes y los cables conectores, lo cual a la larga resulta ser una opción sumamente costosa. Esta debilidad deriva, desde luego, del hecho de que una máquina de estados finitos no es una máquina programable (a diferencia de la máquina Turing que se puede programar usando el hardware que ya se tiene configurado). Pero esto es apenas el principio de las limitaciones de las máquinas de estados finitos. El teorema de Kleene nos afirma que las máquinas de estados finitos sólo son capaces de poder reconocer conjuntos regulares y ninguna otra cosa (léase bien el enunciado del teorema de Kleene). Considérese otro conjunto de hileras como el conjunto:
{0n1n | n≥0}
que contiene hileras como:
01
000111
000000111111
00000000001111111111
Este conjunto de hileras no es un conjunto regular, y por lo tanto no existe ninguna máquina de estados finitos que sea capaz de reconocerlo.
Haciendo una introspección sobre el conjunto de hileras que consta de una cierta cantidad de “ceros” al principio seguida de una cantidad igual de “unos”, posiblemente nosotros en algún momento nos hayamos considerado máquinas de estados finitos, imaginando que nuestros cerebros, constituídos por un número extraordinariamente grande de células, puede tomar un número finito, aunque inmensamente grande, de configuraciones, o estados. Estamos seguros de que si alguien nos presenta una hilera arbitrariamente grande de “ceros” seguida de una cantidad arbitrariamente grande de “unos”, podríamos detectar si el número de “ceros” y “unos” en la hilera es igual.
Para una cantidad pequeña de “ceros” y “unos”, posiblemente nos bastaría con echarle un vistazo a la hilera para decidir si forma parte del conjunto especificado. Así, sin mucho batallar, podemos decir que la hilera 00001111 forma parte del conjunto mientras que la hilera 00111 no forma parte del conjunto. Sin embargo, para una hilera como:
0000000000000000000000000111111111111111111111111
tenemos que recurrir a otro medio de análisis para poder dar una respuesta, y lo más seguro es que recurriríamos a un conteo. Contaríamos el número de “ceros” recibidos, y al llegar el primer “uno” escribiríamos en algún lugar el número de “ceros” contados (o simplemente recordaríamos dicho número en nuestras mentes) para usarlo como referencia futura, y hecho esto empezaríamos a contar el número de “unos” (en rigor de verdad, este es el procedimiento que usamos mentalmente al analizar hileras pequeñas). Pero ahora hemos hecho uso de alguna memoria extra porque una vez que hemos terminado de contar los “unos” tenemos que recordar el número de “ceros” contados para llevar a cabo una comparación. Esto es algo que una máquina de estados finitos no puede hacer, su única capacidad para poder recordar entradas es hacer que un símbolo a su entrada la mande a cierto estado. Supóngase que insistimos en tratar de construír una máquina de estados finitos para poder reconocer la hilera con cantidades iguales de “ceros” y “unos” que hemos visto. Podríamos hacer que cada “cero” vaya moviendo la máquina de estados finitos a un nuevo estado, de modo tal que el conteo de veinte ceros requeriría una máquina que posea por lo menos veinte estados distintos. Sin embargo, puesto que el número de estados en una máquina de estados finitos ya está predeterminado y es un número finito, la estrategia falla en caso de que el número de “ceros” leído sea más grande que ese número finito, y por lo tanto la máquina de estados finitos no puede procesar 0n1n para todos los valores de n. De hecho, si queremos resolver el problema de esta manera usando una computadora digital, nos topamos con el mismo problema, ya que si empezamos con un contador que vaya leyendo la cantidad de “ceros” que hay en la hilera obtendríamos tarde o temprano un sobreflujo porque el contador -formado por una cantidad limitada y finita de registros- sólo puede contar hasta cierto límite. Para poder procesar 0n1n para un n arbitrariamente grande se requiere tener una cantidad ilimitada de memoria auxiliar para poder almacenar tal número, lo cual no puede ocurrir en la práctica.
Otra manera en la cual nosotros como humanos podemos tratar de resolver el problema sería esperar a tener la hilera completa en nuestras manos. Podríamos entonces ir a un extremo de la hilera para tachar un “cero” y luego ir al extremo opuesto de la hilera para tachar un “uno”, regresando al principio de la hilera para tachar otro “cero” y después yendo al extremo opuesto de la hilera para tachar otro “uno” hasta que hayamos agotado todos los “ceros” o todos los “unos”. La hilera pertenecerá al conjunto indicado sí y solo sí hemos agotado todos los “ceros” y todos los “unos” al mismo tiempo. Aunque esta estrategia parece ser diferente de la estrategia anterior, aún así esto requiere recordar cada una de las entradas al tener que regresar para leerlas una vez que la hilera haya sido completada. Y el poder volver a leer las entradas es algo que no puede hacer la máquina de estados finitos.
Tenemos pues para el problema en mano dos procedimientos computacionales diferentes para decidir, dada una hilera de “ceros” y “unos”, si dicha hilera pertenece o no pertenece al conjunto proporcionado. Ambos procedimientos requieren de alguna forma de memoria adicional que no está disponible en una máquina de estados finitos. Resulta evidente que una máquina de estados finitos no es un modelo para la forma más general de un procedimiento computacional. Y tal modelo computacional es proporcionado precisamente por la máquina Turing, la cual puede hacer todo lo que pueda hacer cualquier máquina de estados finitos incluyendo muchas otras cosas que no pueden hacer las máquinas de estados finitos. Vimos en la entrada anterior el diseño de una máquina Turing (especificando los quintuplos requeridos) precisamente la manera de poder reconocer hileras de “ceros” y “unos” que pertenezcan al conjunto 0n1n.
La cinta en la cual ponemos una hilera de símbolos que van a ser reconocidos (procesados) por una máquina Turing sirve como un medio de almacenamiento al poder la cabeza lectora no sólo leer los símbolos de la cinta sino también poder volver a leerlos e inclusive borrarlos para reemplazarlos por otros símbolos. La porción de la cinta que no está en blanco puede ser tan grande como se quiera aunque en cualquier momento dado sólo haya un número finito de espacios que contienen información y que no están en blanco. Por lo tanto, la máquina Turing tiene a su disposición una cantidad ilimitada, aunque siempre finita, de memoria. Las limitaciones de las máquinas de estados finitos no existen para las máquinas Turing, así que las máquinas Turing deben tener capacidades considerablemente mayores que las máquinas de estados finitos, y de hecho, una máquina de estados finitos es un caso especial de una máquina Turing, una que siempre imprime el mismo símbolo previo en la celda que ha sido leída, que siempre se mueve hacia la derecha, y que se detiene al llegar a una celda en blanco. ¿Y en dónde se encuentra almacenado el conjunto de quintuplos que constituye el programa de una máquina Turing? Ciertamente, no en la cinta. Se recuerda aquí que lo que en nuestras ilustraciones parece ser la cabeza lectora de la máquina Turing en realidad es casi la totalidad de la máquina, y en ella es en donde se encuentra almacenado el programa Turing:
Como lo hemos hecho hasta ahora, no se dará aquí una definición formal de los términos “procedimiento computacional”, “procedimiento efectivo” y “algoritmo”. Usaremos estos términos en forma intercambiable echando recurso del concepto intuitivo de lo que es un algoritmo (véase la entrada “Algoritmos computacionales”) o procedimiento efectivo como una “receta” para lograr llevar a cabo cierta tarea. Como hemos visto, un algoritmo debe poseer ciertas características o propiedades. Debe consistir de un listado de instrucciones precisas sobre las acciones que se deberán llevar a cabo en algún lenguaje (inglés, BASIC, JavaScript, etcétera), cada instrucción debe ser finita y la lista en sí también debe ser finita. Cada instrucción debe ser algo que pueda ser llevado a cabo en forma mecánica. Si un algoritmo es un método de solución para cierto problema en particular, entonces, cuando sea aplicado a cierta entrada, el algoritmo eventualmente debe detenerse produciendo la respuesta correcta si es que la respuesta existe. Si no hay respuesta al problema, el algoritmo puede detenerse proclamando que no existe solución al problema que fue presentado, o la máquina puede continuar procesando indefinidamente hasta la misma eternidad buscando una respuesta sin encontrarla.
Hemos visto el uso que se le puede dar a una máquina Turing para resolver el problema del reconocimiento de hileras y la pertenencia de las mismas a cierto conjunto predefinido. Esto es justo lo que se lleva a cabo cuando se parsifica una expresión en un lenguaje de alto nivel como el paso preliminar para convertir las instrucciones en lenguaje de alto nivel a lenguaje de máquina. Si se escribe un programa en lenguaje BASIC que tenga algo como lo siguiente:
10 REM UN PROGRAMA EN BASICy se presenta el programa a un compilador BASIC, entonces al llegar a la segunda instrucción el compilador encontrará la palabra castellana “PASO” (en lugar de la palabra inglesa que esperaría encontrar, STEP), y decidirá por medio de un simple procedimiento comparativo al buscar en su “diccionario” de palabras reservadas que la palabra PASO no pertenece al conjunto de palabras reservadas en BASIC para enunciados de control, tras lo cual rechazará el programa emitiendo un mensaje de error.
20 FOR X = 1 TO 20 PASO 5
30 PRINT "HE AQUI UN PROGRAMA BASIC"
40 NEXT X
50 END
Nos falta ver otro aspecto importante de las máquinas Turing, usando dichas máquinas no para reconocer hileras de símbolos (el paso crucial para el manejo de los lenguajes de programación en lo que es conocido como la Teoría de los Lenguajes Formales), sino como computadoras de función para resolver problemas de índole matemática. En particular, ¿es posible encontrar siempre una máquina Turing para resolver cualquier procedimiento algorítimico que pueda ser concebido por el hombre?