La capacidad para poder contar, una capacidad que requiere forzosamente el conservar información en algún tipo de registro o de memoria, es lo que pone a la máquina Turing muy por encima de las máquinas de estados finitos que no poseen tal capacidad. Gracias a ello, la máquina Turing posee la capacidad para poder reconocer hileras de símbolos, lo cual representa el primer paso para el reconocimiento de palabras y la construcción de gramáticas.
Veremos ahora otra faceta de las máquinas Turing, usándolas como computadoras de función para resolver problemas de índole matemática, con lo cual cerraremos un círculo importante.
Antes de usar una máquina Turing T para resolver un problema matemático, tenemos que ser realistas respecto a los problemas matemáticos que la máquina sea capaz de resolver. Si queremos que la máquina T lleve a cabo la adición de dos números enteros finitos, podemos suponer que la máquina T eventualmente se detendrá al haber terminado la tarea que le fue encomendada. Pero si queremos que la máquina T obtenga la secuencia completa de dígitos numéricos de los que consta el número pi (π.≈.3.1416), estaremos ante una imposibilidad, porque la secuencia de dígitos numéricos de π es infinitamente grande. Podemos pedirle a la máquina T que calcule los primeros cien dígitos de π, lo cual hará y lo cual sabremos cuando la máquina se haya detenido. Podemos pedirle también que nos calcule los primeros cien mil dígitos, lo cual también hará y lo cual también sabremos cuando la máquina T se haya detenido. Pero si le pedimos que vaya calculando cada dígito numérico de π sin imponer limitante alguna, la máquina T tal vez proceda con el cálculo de cada dígito pero sin detenerse jamás. Obviamente, el criterio de la detención será el parámetro más importante para decidir cuáles problemas son solubles y cuáles son irresolubles.
El conjunto de quintuplos que define alguna máquina Turing puede ser modificado de modo tal que cuando la máquina vaya a detener su marcha en un estado que no es un estado final de aceptación, la máquina entre en un nuevo estado que ocasione que la cabeza lectora continúe moviéndose hacia la derecha sin detenerse jamás. Por lo tanto, podríamos haber definido el reconocimiento de un conjunto S de hileras diciendo que la máquina T se detiene cuando es puesta en marcha actuando sobre una hilera que forma parte del conjunto S, y no se detiene cuando es puesta en marcha actuando sobre una hilera que no forma parte del conjunto S. De este modo, el criterio de no-aceptación en lugar de ser “detenerse en un estado que no es el estado final” vendría siendo “no detenerse”. Sin embargo, no podemos hacer lo contrario, porque tal vez no podamos reconocer cada situación de “no detenerse” convirtiéndola a una detención en un estado no-final.
Si un conjunto S es reconocido por una máquina Turing T, se dice que tenemos un procedimiento efectivo (un algoritmo, una “receta de cocina”) para poder ir generando una lista de las hileras que pertenecen al conjunto S. Podemos hacer muchas copias de la máquina T, tales como T1, T2, T3, y así sucesivamente, y echar a andar dichas máquinas con cintas conteniendo hileras α1, α2, α3, y así sucesivamente. Periódicamente, regresaríamos para checar el estado de cada una de las máquinas. Cuando una máquina se haya detenido en un estado final de aceptación, sabemos que la hilera puesta en la cinta forma parte del conjunto S. Pero para aquellas máquinas en las que el cómputo sigue en marcha, en general no podemos saber si las hileras en las cintas pertenecen o no al conjunto S de hileras, porque el procesamiento puede detenerse o puede no detenerse en un tiempo posterior indefinido. Supóngase sin embargo que el conjunto S de hileras es reconocido por una máquina Turing T que se detiene en todas las hileras de entrada (como las hileras formadas por cierta cantidad de “ceros” seguidas de una cantidad igual de “unos”). En tal caso se tiene un procedimiento efectivo para decidir la membresía de una hilera en el conjunto S. Tomamos cualquier hilera α y hacemos que la máquina Turing T actúe sobre ella. El cómputo eventualmente se detiene. Si la máquina Turing T se detiene en un estado final, entonces la hilera α pertenece al conjunto S, y si se detiene en un estado no-final, la hilera no pertenece al conjunto S.
Hay una diferencia sutil entre generar los miembros de un conjunto S y decidir la pertenencia a un conjunto. Hay conjuntos para los cuales podemos construír máquinas Turing que los reconocerán, de modo tal que se tiene un procedimiento efectivo para ir generando sus miembros, pero no hay máquina Turing que permita decidir membresía llegando a un estado de detención en todas las entradas que se le proporcionen.
Habiendo visto cómo podemos usar una máquina Turing T para reconocer hileras, giramos nuestra atención a otra característica que distingue a las computadoras, su capacidad para llevar a cabo cálculos numéricos. Podemos pensar de la máquina T como una máquina que evalúa funciones numérico-teóricas. Dada una máquina Turing T y una hilera α de símbolos en la cinta, empezamos con la máquina puesta en la configuración inicial convencional (cabeza lectora situada en el extremo izquierdo de la cinta en el primer símbolo que no es un espacio en blanco) actuando sobre una cinta que contiene a la hilera α. Si después de una secuencia finita de pasos la máquina se detiene con otra hilera β puesta en la cinta, podemos considerar a β como el valor de una función evaluada sobre α, o sea T(α).=.β. Usando la terminología de los matemáticos, el dominio (el alcance o cobertura) de la función consiste de todas las hileras α para las cuales la máquina T eventualmente se detiene al terminar su tarea.
Por cuestiones de conveniencia, adoptaremos una notación mediante la cual poniendo una barrita horizontal encima de un número decimal o un símbolo se interpretará como una hilera formada por n+1 “unos”. Esta notación es conocida como la representación unaria de un entero no negativo. De este modo, si n.=.4, entonces:
n = 4 = 11111
Suponiendo que el símbolo del asterisco (*) forma parte del alfabeto de símbolos que se pueden poner en una cinta (y el cual será utilizado como delimitador para separar un número de otro), entonces una cinta que contenga la hilera:
n1*n2*n3*··· nk
puede ser vista como la representación en la cinta de un k-tuplo de enteros positivos (n1,n2,...,nk). Si la máquina T es puesta en marcha en la configuración inicial convencional (con la cabeza lectora posicionada en el extremo izquierdo de la cinta sobre el primer símbolo que no es un espacio en blanco) y la cinta final al detenerse con la representación unaria m de un entero positivo m, entonces la máquina T ha actuado como una función de Tk de k variables:
Tk(n1*n2*n3*··· nk) = m
Si la máquina T no se detiene o se detiene cuando la hilera en la cinta final no es la representación de un entero positivo, entonces la función Tk no está definida para el k-tupla (n1*n2*n3*··· nk) que le haya sido proporcionado.
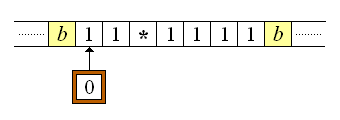
Considérese una máquina Turing T definida por el siguiente par de quintuplos:
(0,1,1,0,D)Si empezamos la máquina T en configuración inicial convencional (cabeza lectora situada en el extremo izquierdo de la cinta en el primer símbolo que no es un espacio en blanco), entonces si se le proporciona a la máquina T la siguiente hilera de entrada:
(0,b,1,1,D)
la máquina se detendrá en la siguiente configuración final:
Podemos mostrar lo que sucede con el siguiente gráfico animado:
En este caso, la máquina define una función matemática de una variable que hace un mapeo de la hilera 11111 a la hilera 111111, que con la notación unaria podemos representar como:
T(4) → 5
En general, para cualquier hilera, la máquina T que se acaba de describir hace el siguiente mapeo:
T(n) → n+1
Hablando en términos aritméticos, se trata de una función muy sencilla, una función de una sola variable que consiste en tomar un entero positivo y sumarle 1.
Tenemos, pues, una máquina Turing de cómputo aritmético sencilla que puede tomar un entero positivo sumándole una unidad. Con la misma facilidad podemos diseñar una máquina Turing que le sume al entero positivo dos unidades, o tres unidades, o la cantidad que sea. En esencia, hemos resuelto la interrogante sobre cómo sumar a un entero positivo una constante numérica.
El siguiente paso sería aprender a programar una máquina Turing para sumar dos enteros positivos n1 y n2, o sea calcular la función:
f.(n1,n2) = n1 + n2
Si separamos las representaciones unarias de los números n1 y n2 con un símbolo asterisco (*), una manera de obtener la suma de los dos enteros (entre muchas otras posibles) está dada por el siguiente conjunto de quintuplos:
| (0,1,b,1,D) | Al empezar, se borra un "1", el primer "1" que hay en el extremo izquierdo, poniendo un espacio en blanco en donde estaba el "1" |
| (1,*,b,3,D) | En caso de que n1 sea igual a cero, la máquina es puesta en su estado final 3 |
| (1,1,1,2,D) (2,1,1,2,D) (2,*,1,3,D) |
En el caso en el que n1
es mayor que cero, simplemente se borra el símbolo delimitador (*) poniendo en su lugar un "1", reemplazando de este modo el "1" que fue borrado al principio en el extremo izquierdo |
En este procedimiento efectivo de resolución, para llevar a cabo la suma se recurre a un truco aprovechando la representación unaria de los dos números n1 y n2. Simplemente se borra el símbolo delimitador (el asterisco *) puesto entre los dos números unarios poniendo un “1” en su lugar, habiendo borrado previamente el “1” correspondiente a la representación unaria de n1 situado en el extremo izquierdo de la cinta. Esta operación une las dos hileras, produciendo un número que en notación unaria corresponde al número que resulta de la suma de n1 y n2. De este modo, si se tiene 4 = 11111 para n1 y 3 = 1111 para n2, entonces si en la cinta se tenía 11111*1111 al principio al final se tendrá la hilera 111111111, que es la representación unaria de 8 y que a su vez es la suma de los dos números n1 y n2. Obsérvese que en este ejemplo la cabeza lectora de la máquina siempre se mueve de izquierda a derecha, nunca en sentido contrario.
Sumar es una cosa, y restar es otra. ¿Podemos definir un procedimiento para tomar un entero positivo restándole otro entero (que supondremos más pequeño para evitar por lo pronto el tener que lidiar con números negativos)? La respuesta es afirmativa. Incluso podemos tomar una expresión numérica que conste de dos variables restándole cierta cantidad a una de ellas e ignorando la otra. Considérese la siguiente función de dos variables n1 y n2 que son enteros positivos:
f.(n1, n2) = n2 - 1
para la cual supondremos que n2 es un entero diferente de cero, y para el caso en el que n2 sea igual a cero supondremos que la función es indefinida. Usando la representación unaria de enteros no-negativos, la siguiente máquina Turing es una entre muchas otras que puede llevar a cabo la tarea deseada:
| (0,1,1,0,D) (0,*,*,1,D) |
Con este par de quintuplos pasamos por encima de n1 y por encima del símbolo delimitador asterisco (*) hasta llegar finalmente al número n2 |
| (1,1,1,1,D) | Con este quintuplo se cuenta el primer "1" que hay en n2 |
| (2,b,b,3,D) | En caso de que n2
= 0, la máquina se detiene, al no haber quintuplos que definan alguna acción a tomar cuando el estado de la máquina es 3 |
| (2,1,1,4,D) (4,1,1,4,D) (4,b,b,5,I) |
El movimiento constante hacia la derecha prosigue sin cambios en la cinta hasta encontrar el extremo derecho de la hilera n2 |
| (5,1,b,6,I) | Borrar el último "1" en n2 efectuándose así la operación de substracción |
| (6,1,1,6,I) (6,*,b,7,I) |
Pasar hacia la izquierda de n1
borrando el símbolo asterisco delimitador (*) |
| (7,1,b,7,I) | Ir borrando el número n1 |
| (7,b,b,8,I) | Al terminar de borrar el número n1 detener el avance de la cinta al llegar al estado final de la máquina, dejando el resultado final del cómputo en la cinta |
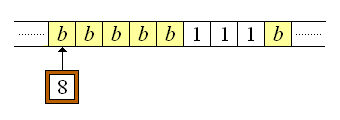
No resulta difícil comprobar que si dada la hilera 11*1111 (que en la representación unaria simboliza los números enteros 1 y 3, respectivamente, usando el símbolo asterisco como delimitador entre ambos números) empezamos la máquina Turing del modo convencional:
entonces la máquina Turing se detendrá en la siguiente configuración:
Obsérvese que en la cinta se han borrado los números unarios n1 (11) y n2 (1111) así como el símbolo asterisco (*) usado como delimitador entre ambos números, y sólo aparece el número unario 111, que equivale al entero 2. En efecto, se ha realizado el cómputo:
f.(1,3) = 3 - 1 = 2
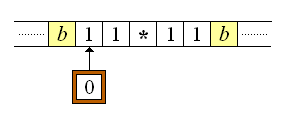
Por otro lado, si empezamos con la hilera 11*1 que en la representación unaria simboliza los números 1 y 0 separados por el asterisco delimitador:
entonces la máquina Turing se detendrá en la siguiente configuración:
Puesto que la hilera final en la cinta, en la cual subsiste el símbolo asterisco delimitador, no es la representación unaria de número entero alguno, la función computada por la máquina Turing es indefinida en (n1,n2) = (1,0), tal y como lo habíamos especificado desde un principio.
Veamos ahora otro ejemplo parecido al anterior, el de una máquina Turing que toma una función de tres variables n1, n2 y n3, regresándonos la adición de 1 al entero n2 cuando n2 es mayor que cero, y dejando la función indefinida para el caso en el cual n2 es igual a cero, o sea:
f.(n1,n2,n3) = n2 + 1 para n2.>.0
un conjunto de quintuplos (entre muchos otros posibles) que puede llevar a cabo la tarea es el siguiente:
(0,1,b,0,D)Un ejercicio un poco más interesante, que involucra a una sola variable numérica, es el de encontrar una máquina Turing que dado un entero positivo n cualquiera pueda obtener el doble de dicho número, o sea 2n. Un conjunto de quintuplos que puede llevar a cabo esta tarea es el siguiente:
(0,*,b,1,D)
(1,1,1,2,D)
(2,*,*,3,D)
(3,1,1,2,I)
(2,1,1,4,D)
(4,1,1,4,D)
(4,*,1,5,D)
(5,1,b,5,D)
(5,b,b,6,D)
| (0,1,1,1,D) (1,b,b,8,D) |
Para el caso en el que n sea igual
a cero, se calcula trivialmente 2·0 = 0 y la máquina pasa al estado final de detención |
| (1,1,1,2,D) (2,1,1,2,D) (2,b,b,3,I) |
Para el caso en el que n sea mayor
que cero, encontrar el lado extremo de n |
| (3,1,X,4,D) (4,X,X,4,D) (4,1,1,4,D) (4,b,1,5,I) |
Se pone una "tacha"
cambiando el "1" a un símbolo X, agregando un "1" en el extremo derecho de la hilera |
| (5,1,1,5,I) (5,X,X,6,I) (6,X,X,6,I) (6,1,X,4.D) |
Ejecutar un movimiento hacia la izquierda hasta dar con el siguiente "1" del número unario n |
| (6,b,b,7,D) (7,X,1,7,D) (7,1,1,8,D) |
Con este trío de quintuplos n es doblado al ser cambiadas las tachas "X" a "1", siendo puesta la máquina en su estado final 8 |
PROBLEMA: Encuéntrese una máquina Turing que sea capaz de calcular la siguiente función:
f(n) = n - 2 para n.≥.2
f(n) = 1 para n.<.2
Un conjunto de quintuplos que puede efectuar el cómputo pedido es el siguiente:
| (0,1,1,1,D) | Leer el primer "1" |
| (1,b,1,6,D) | En caso de que n sea igual a cero, cambiar a "1" y poner a la máquina en en el estado final 6 |
| (1,1,1,2,D) | Leer el segundo "1" |
| (2,b,b,6,D) | En caso de que n sea igual a 1, poner a la máquina en el estado final 6 |
| (2,1,1,3,D) | Cambio del estado 2 al estado 3 en caso de que n ≥ 2 |
| (3,1,1,3,D) (3,b,b,4,I) |
Moverse hasta encontrar el extremo derecho de n |
| (4,1,b,5,I) (5,1,b,6,I) |
Borrar dos "1" de la representación unaria n, y detener la máquina en el estado final 6 |
Un cierto tipo de problemas que recurre con frecuencia es el de encontrar entre dos o más cantidades cuál de ellas es la mayor. Expresado notacionalmente, esto equivale a la evaluación de la función:
f.(n1,n2) = max(n1,n2)
¿Podemos diseñar una máquina Turing que lleve a cabo esta evaluación para dos enteros positivos? La respuesta es afirmativa. Un conjunto de quintuplos que puede llevar a cabo lo anterior (entre otros posibles) es el siguiente:
| (0,1,X,1,D) | Este quintuplo cambia el primer "1" de la representación unaria de n1 poniendo una "X" en su lugar |
| (1,1,1,1,D) (1,*,*,2,D) (2,X,X,2,D) (2,1,X,3,I) |
Se pasa por encima de los "1" y del símbolo delimitador asterisco (*) para encontrar el "1" más a la izquierda de n2 cambiándolo a una "X" |
| (3,X,X,3,I) (3,*,*,4,I) (4,1,1,4,I) (4,X,X,5,D) (5,1,X,1,D) |
Caminando hacia la izquierda y pasando por encima de las "X" y del símbolo delimitador asterisco, se encuentra el "1" más a la izquierda de n1, cambiándolo a "X" |
| (5,*,*,6,D) | Con n1
agotado, se llega a la determinación de que n2 ≥ n1 |
| (6,X,1,6,D) (6,1,1,7,I) (6,b,b,7,I) |
Cambian las "X" en n2
a "1" al haberse determinado que este es el mayor de los dos números enteros |
| (7,1,1,7,I) (7,*,b,7,I) (7,X,b,7,I) (7,b,b,10,I) |
Se borran la hilera n1
y el símbolo asterisco delimitador (*), deteniendo la máquina en el estado final 10 |
| (2,b,b,8,I) | Con n2
agotado, se llega a la determinación de que n1 ≥ n2 |
| (8,X,b,8,I) (8,*,6,9,I) |
Se borra la hilera n2 |
| (9,X,1,9,I) (9,b,b,10,I) |
Cambian las "X" en n1 a
"1" al haberse determinado que este es el mayor de los dos números enteros, deteniéndose la máquina en el estado final 10 |
En lo poco que hemos visto, parece que debe de haber una máquina Turing adecuada a cada problema, siempre y cuando haya una “receta de cocina”, un algoritmo (véase la entrada “Algortimos computacionales”) con el que podamos definir algún conjunto de quintuplos. Esto presupone, desde luego, que siempre habrá una máquina Turing capaz de poder ejecutar cada algoritmo que se nos ocurra. ¿Pero qué nos garantiza ésto? La máquina Turing, desde luego, es un concepto matemáticamente preciso, definido sin ambigüedad alguna a partir del momento en el que se define el quintuplo generalizado. El problema es que no podemos dar una definición igualmente precisa de lo que es un algoritmo, ya que hay algoritmos para muchas cosas tales como la extracción de la raíz cuadrada de un número, el ordenamiento alfabético de un listado de artículos, o el reconocimiento de ciertas palabras predeterminadas. Con tal variedad de aplicaciones, ¿cómo vamos a darle a un algoritmo, a un procedimiento efectivo de resolución, una definición matemáticamente precisa? Aunque intuitivamente nos resulte claro lo que es un procedimiento efectivo de resolución, otra cosa muy distinta es tratar de definir tal concepto en términos matemáticamente precisos. Es algo así como el amor, todos sabemos lo que es, pero nadie puede darle una definición lógico-matemática precisa. En vista de tal imposibilidad, parece ser igualmente imposible el poder pronosticar de antemano cuáles algoritmos pueden ser implementados por máquinas Turing y cuáles no. Como igualmente sorprendente resulta ser la siguiente aserción:
Dada cualquier función numérico-teórica que pueda haber para la cual exista un procedimiento efectivo de resolución, siempre habrá una máquina Turing que pueda llevar a cabo la implementación del algoritmo.Esta es una aserción categórica. No está afirmando que “tal vez” pueda haber una máquina Turing para cada procedimiento efectivo de resolución. Se está afirmando que siempre habrá una máquina Turing para ello. Dado algo intuitivo y nebuloso, la resolución llevada a cabo por una máquina Turing se dá por hecho, dada la existencia de un procedimiento efectivo, la existencia de la máquina Turing encargada de implementarlo mecánicamente sin que haga falta nada está garantizada:
El problema de dar con una máquina Turing para cierto algoritmo rebuscado puede ser un problema de los mil demonios, pero tal máquina Turing siempre existirá. Esta afirmación fue asentada tanto por Alan Turing como por quien fue su maestro, el matemático Alonzo Church (el inventor del cálculo lambda). Sin embargo, no produjeron una demostración de ello, se resignaron a dejarla asentada como una tesis, hoy conocida como la tesis de Church-Turing.
A diferencia del concepto de procedimiento efectivo, el cual es un concepto intuitivo y por lo tanto nebuloso, el concepto de la máquina Turing es un concepto matemático preciso, y puesto que no es posible establecer de modo formal una equivalencia entre un concepto intuitivo y un concepto matemático preciso, el enunciado Church-Turing debe permanecer por siempre como una tesis, como algo que se supone cierto pero cuya demostración formal es una imposibilidad. Una “prueba” de la validez de la tesis Church-Turing es que hasta la fecha nadie ha podido especificar un algoritmo que no pueda ser ejecutado mecánicamente por una máquina Turing, por más que muchos se han abocado a encontrarlo.
Aunque el lector no se haya dado cuenta de ello, desde los primeros días en los que comenzó a aprender a usar una computadora ha estado poniendo en práctica una buena cantidad de algoritmos. El abrir cierto programa (por ejemplo, un programa de retoque de imágenes) y usarlo para lograr cierto resultado requiere de un número finito de pasos aplicados siguiendo cierto orden, y si se ejecuta un paso equivocado o no se sigue el orden correcto, entonces no se llega al resultado deseado. Las veces que el lector haya pedido ayuda a un instructor o un maestro al quedar atorado en el uso de un programa se debieron a que el algoritmo requerido para la resolución del objetivo (problema) no era el adecuado, y la ayuda recibida consistía en obtener la secuencia correcta de pasos a seguir para poder llegar al resultado deseado. Desde que se enciende la computadora hasta que se apaga, todo, absolutamente todo, es una gran colección de algoritmos, trátese del algoritmo requerido para poner la computadora en estado de hibernación bajo cierto sistema operativo, trátese del algoritmo requerido para copiar un archivo del disco duro a un dispositivo USB, trátese del algoritmo requerido para crear cierta tabla o para usar cierto compilador en un lenguaje de alto nivel.
La otra cara de la moneda de la tesis Church-Turing es que si no se puede especificar un procedimiento efectivo de resolución para algún problema, entonces no existe, ni siquiera en principio, ninguna máquina en todo el Universo que será capaz de resolver tal problema, sin importar lo poderosa que pueda ser. La máquina Turing es lo que fija el límite supremo sobre lo que se puede hacer y lo que no se puede hacer con las máquinas de cómputo. Si una computadora puede ejecutar cierto algoritmo, cualquier otra computadora bajo cualquier otro sistema operativo lo puede hacer también, al ser ambas equivalentes a una máquina Turing, y lo que no se pueda hacer en una (aunque se cuente con una memoria lo suficientemente grande para tal efecto) tampoco se puede hacer en ninguna otra.
La tesis Church-Turing es aceptada hoy en día como una herramienta de trabajo en el área de computabilidad efectiva. Si en un trabajo de investigación se describe un algoritmo para llevar a cabo el cálculo matemático de una función y el algoritmo parece ser un procedimiento efectivo, entonces invocando la tesis Church-Turing se dá por hecho que debe ser posible especificar una máquina Turing para llevar a cabo el cálculo de la función. Aunque la tesis Church-Turing está enunciada teniendo en mente funciones numérico-teóricas, se le puede dar una interpretación más amplia. Cualquier procedimiento efectivo que involucre una manipulación de un conjunto finito de símbolos puede ser traducida a una función numérico-teórica llevando a cabo una codificación apropiada de los símbolos considerándolos como enteros positivos. De este modo, invocando la tesis Church-Turing, podemos afirmar que si existe un procedimiento efectivo para llevar a cabo una tarea que involucre una manipulación de símbolos, entonces existe una máquina Turing para efectuar de modo completamente mecánico la tarea. La aceptación de la tesis Church-Turing conlleva la aceptación de la máquina Turing como el modelo supremo de un dispositivo efectivo de cómputo. Por algún tiempo se llegó a sospechar que podía haber un modelo superior de cómputo que podía llevar a cabo tareas que la máquina Turing era incapaz de hacer, lo cual suponía que “algo” le faltaba a la máquina para poder cubrir todas las posibilidades, para lo cual era necesario encontrar algún procedimiento incapaz de ser llevado a cabo por una máquina Turing pero capaz de ser llevado a cabo por una máquina superior. Hasta la fecha nadie ha podido encontrarlo. Teóricamente, las capacidades de cómputo de la máquina Turing superan cualquier cosa que pueda hacer cualquiera de las computadoras de nuestra actualidad que ciertamente no poseen la capacidad ilimitada de memoria de una máquina Turing, siendo extraordinario el hecho de que este modelo fue descubierto en 1936, mucho antes de la llegada de las computadoras de hoy en día.
Al apelar a la tesis Church-Turing para cualquier situación que se pueda dar, estamos poniendo mucha confianza y mucha fé en algo cuya validez, a fin de cuentas, no se puede probar teóricamente de modo riguroso y formal. Hasta la fecha, nadie ha podido encontrar un procedimiento efectivo que no pueda ser implementado en una máquina Turing, pero ello no significa que dentro del universo infinito de posibilidades tal cosa no exista, quedando por siempre la sospecha y la duda. Este dilema que se tiene con la tesis Church-Turing que no es un teorema que pueda ser demostrado sino una tesis que aceptamos con mucha fé no es muy diferente a una situación de mayor fondo descubierta por Kurt Gödel que tiene que ver con la reina de las ciencias, las matemáticas. Una de las suposiciones con las que trabajan los matemáticos es que, partiendo de un mismo conjunto de axiomas, y aplicando correctamente la lógica sin incurrir en equivocaciones, no es posible obtener dos respuestas diferentes a un mismo problema. Ciertamente, en los exámenes de fin de curso muchos estudiantes tienen la oportunidad de comprobar por sí mismos que no hay dos respuestas distintas (contradictorias) a un mismo problema, y si las hay, una de ellas necesariamente tiene que estar en el error. De lo que estamos hablando es de la consistencia de las matemáticas. Por buen tiempo se creyó que, siendo las matemáticas consistentes, habría alguna manera de poder demostrar teóricamente dicha consistencia. Pero con los teoremas de Gödel quedó demostrado formalmente que no es posible, ni siquiera en principio, el poder demostrar que la aritmética es consistente (partiendo de un conjunto básico de postulados lo suficientemente fuerte para poder generar los números naturales). Ello no significa que las matemáticas puedan producir algún día resultados contradictorios. Significa simplemente que no hay forma alguna de garantizar que nunca se obtendrá algún día un par de resultados contradictorios. Se teme desde luego, que algún día un matemático trabajando en un teorema suyo quizás llamado “teorema de los números primos impares” obtenga una respuesta que contradiga a otro teorema quizás llamado “divisibilidad de números diofantinos bajo una aritmética modular sin residuos”. Si tal cosa ocurriera, ello haría tambalear la pirámide, ¡y vaya que se ha construído mucho en torno a esa pirámide! Hasta la fecha, ello no ha ocurrido, pero ello no es garantía de que no pueda ocurrir, de que tarde o temprano caerá la manzana de la discordia que terminará agüando la fiesta. Se ha dicho sobre esto que “Dios existe porque la aritmética es consistente, el Diablo existe porque no podemos demostrarlo”.
En su trabajo original, Gödel, habla “sobre las proposiciones formalmente indecidibles”, proposiciones aritmético-lógicas cuya demostración no es posible. A diferencia del teorema de Pitágoras, que puede ser demostrado como verdadero recurriendo a una simple aplicación de triángulos congruentes y a los axiomas en los que se asienta la geometría Euclideana, hay proposiciones cuya veracidad o falsedad no es posible demostrar. Tales proposiciones necesariamente tienen que ciertas o tienen que ser falsas, pero esto no es posible saberlo ni siquiera en teoría, al menos no por derivaciones formales. Invocando la tesis Church-Turing, al no haber un procedimiento efectivo que pueda demostrar la veracidad o falsedad de tales proposiciones formalmente indecidibles, tampoco es posible construír una máquina Turing que lo haga. ¿Y cómo podría hacerlo, si no hay un procedimiento efectivo de resolución para tales casos con el que pueda ser programada? Sin embargo, hay una manera de darle vuelta al asunto. Se puede poner en marcha una computadora para ir evaluando diversas combinaciones numéricas para algunas de tales proposiciones formalmente indecidibles. Basta con encontrar un solo ejemplo numérico (por ejemplo, un número como 43924652) en el que no se cumpla la proposición para rechazarla como una verdad absoluta. El problema es que no hay garantía alguna de que la máquina se detendrá después de varios siglos de estar probando numerosas posibilidades. Y si la máquina se detiene encontrando la excepción que manda abajo la regla, podemos tomarlo como una “demostración” aunque no se trate de una demostración que haya partido de un conjunto aceptado de axiomas sino más bien de una proeza de la fuerza bruta que resulta de haber llevado a cabo trillones de cálculos.
Iremos ahora tras algo un poco más ambicioso. Hemos visto ya que se puede construir una máquina Turing para cada tipo de problema ya sea de reconocimiento o de cómputo, ¿pero cómo podríamos arreglarnosla para construír una máquina que sea capaz de simular a todas las demás máquinas Turing, una especie de super-máquina, algo así como una máquina Turing universal?
Tomando nuevamente a la máquina Turing como un dispositivo para llevar a cabo cálculos matemáticos, supongamos que tenemos una máquina Turing T viéndola como una computadora para la función f (por ejemplo, la extracción de la raíz cuadrada de un número). Una forma trivial de obtener otra máquina T’ que lleve a cabo la misma evaluación consiste en añadir quintuplos adicionales a la definición original de T que representen pares de estados y entradas que jamás serán encontrados al procesar la función matemática. Esto nos puede producir una variedad infinita de máquinas T que lleven a cabo el cómputo de la misma función. Otra posibilidad es una con la que los programadores están familiarizados, consistente en buscar y encontrar un algoritmo diferente que pueda llevar a cabo el mismo cómputo, habido el hecho de que frecuentemente hay varias maneras de lograr el mismo fin. Hasta este punto, hemos logrado simular las acciones de cualquier máquina de estados finitos con el solo hecho de poner en marcha la máquina Turing programada de acuerdo a los quintuplos especificados. El procedimiento de ir buscando entre la lista de quintuplos aquél quintuplo que corresponda al estado presente de la máquina y al símbolo que está siendo leído o bien detener la máquina en caso de no existir tal quintuplo podemos tomarlo con todo rigor como un procedimiento efectivo. Entonces, invocando la tesis Church-Turing, si existe éste procedimiento efectivo que puede correr en cualquier máquina Turing sobre cualquier entrada proporcionada, debe existir una máquina Turing especial capaz de poder simular las acciones de cualquier máquina Turing T trabajando sobre cualquier entrada que le sea proporcionada a la máquina T. Esta máquina especial es lo que llamamos una máquina Turing universal que simbolizaremos como U.
Para que la máquina Turing universal U pueda llevar a cabo una simulación de las acciones de una máquina T actuando sobre una hilera de entrada α, la máquina U tiene que tener conocimiento de la descripción de T, o sea de los quintuplos que la definen, así como de la hilera α. Puesto de otro modo, lo que servirá de entrada a la máquina U es el par ordenado (T,α). Tenemos que decidir ahora cómo codificar (escribir) esta información en la cinta usada por la máquina U. Supóngase que la acción de la máquina T está ordenada por los siguientes quintuplos:
(0,0,1,0,D)los cuales actuarán sobre la hilera:
(0,1,0,0,I)
α = ···bb10bb···
De este modo, juntando en la cinta de la máquina U los quintuplos de T y la hilera α leída por T, lo que se quiere es poner en la cinta de la máquina U, codificado de algún modo, es lo siguiente:
···bb0010D*0100D**10bb···
Para lograr la codificación, podemos separar en la cinta de la máquina U cada componente de cada quintuplo del otro componente del mismo quintuplo con el símbolo delimitador *, y separar un quintuplo del otro con un par de símbolos delimitadores (**), seguidos de la hilera α y separando dicha hilera α de los quintuplos con un triple de símbolos delimitadores (***). Asimismo, podemos codificar el símbolo “D” (movimiento hacia la derecha) con un par de “unos”, y codificar el símbolo “I” (movimiento hacia la izquierda) como un “uno”. De este modo, usando como ejemplo a los quintuplos y la hilera dados arriba, y con la ayuda de la representación unaria usada arriba, podemos escribir lo siguiente en la cinta de la máquina U:
···b1*1*11*1*11**1*11*1*1*1***11*1*b···
Aunque lo anterior parece suficiente, no lo es. La máquina U también tiene que tener conocimiento de la posición P actual de la cabeza lectora de la máquina T que está simulando. Y por último, la máquina U necesita de algún “espacio de trabajo” para mantenerle la pista al estado presente y al símbolo de la máquina T que están siendo leídos. separado del resto con algún símbolo como W. Adoptando estas convenciones, la hilera en la cinta de la máquina universal U sobre la cual se trabajará al iniciar la simulación de T será algo como lo siguiente:
El funcionamiento de la máquina universal U es llevado a cabo en ciclos, y cada ciclo de U representa un paso individual en los cómputos de la máquina T actuando sobre una hilera α. La forma en la que trabaja la máquina U es la siguiente: la máquina U busca en la lista de quintuplos que corresponden a la máquina T comparando los primeros dos símbolos de un quintuplo de T con los dos símbolos en su espacio de trabajo. Si no se encuentra una pareja idéntica, entonces se sabe que la máquina T debe detenerse, y por lo tanto también la máquina U se debe detener. Si se encuentra un par correspondiente, entonces la máquina U debe cambiar el símbolo que le sigue al símbolo de posición P al tercer símbolo que haya en el quintuplo de T referido, lo cual vendría siendo el nuevo símbolo impreso en la cinta de la máquina T. Hecho esto, se cambiará el símbolo que sigue a W al cuarto componente que obra en el quintuplo, siendo éste el nuevo estado de la máquina T que está siendo simulada por la máquina U. Esto moverá a P algún número de celdas hacia la izquierda o hacia la derecha dependiendo del último símbolo (el que especifica el sentido del movimiento de la cabeza lectora). Finalmente, copiará al nuevo símbolo que ahora sigue a P hacia el segundo bloque detrás del marcador W del espacio de trabajo para mostrar cuál nuevo símbolo de la cinta está siendo leído por la máquina T.
Así pues, la máquina U está simulando lo que la máquina T hace con sus propios quintuplos sobre la hilera que le es proporcionada a T. La entrada de la máquina U es (T,α). Después de varios ciclos llevados a cabo por la máquina U, los quintuplos de T permanecerán intactos en la cinta pero la hilera α habrá sido modificada para reflejar la acción simulada de la máquina T actuando sobrer la hilera α. Bajo el esquema que se ha dado, la máquina U debe poder crear espacio adicional a la mitad de la cinta moviendo algunos símbolos hacia la izquierda o hacia la derecha. Este paso adicional es requerido en caso de que la máquina T en su nuevo estado tenga alguna representación en notación unaria que sea más grande que lo que se tenía previamente, y se requiere de mayor espacio después del marcador W.
Se han descrito las acciones generales que debe llevar a cabo una máquina U. Naturalmente, la máquina Turing universal U debe tener también sus propios quintuplos con los cuales estará trabajando. Escribir los quintuplos de U para que pueda llevar a cabo las acciones que se han descrito sería tedioso, pero no difícil. La máquina Turing universal U nos proporciona una sola máquina capaz de poder simular cualquier otra máquina Turing T cuando se le proporcionan los quintuplos de T y los datos sobre los cuales trabajará. En lugar de construír una máquina Turing para hacer cada trabajo, podemos construír la máquina Turing universal y programarla para hacer diversos trabajos. Y esto es quizá lo más trascendental, el hecho de que los quintuplos de la máquina T sean sacados fuera de la unidad de estados finitos de la que forma parte la cabeza lectora, y que tales quintuplos sean codificados dentro de la cinta de la máquina U. Esto responde una interrogante que nos podríamos haber formulado desde un principio: ¿por qué no poner los quintuplos (o sea, el programa) en la misma cinta de la máquina?:
Esta idea que parece tan sencilla tiene repercusiones enormes, ya que es precisamente lo que posibilita la construcción de una máquina que pueda funcionar como máquina universal capaz de poder correr cualquier tipo de programa. En realidad, se trata de lo mismo que propuso John von Neumann en 1947 (véase la entrada “La arquitectura fundamental”), esto es, mover lo que define al programa de la máquina de un laberinto de alambres y componentes electrónicos fijos interconectados a lo que es la memoria modificable y de acceso rápido de la máquina. Sin esta idea de hondas repercusiones, aún estaríamos atorados con máquinas de capacidades sumamente limitadas en comparación con las máquinas programables de las que disponemos ahora.
Para darnos una idea de la relevancia del paso que se ha tomado, considérese la máquina Turing que fue discutida en detalle en la entrada “La máquina Turing I” que determina si una hilera de “unos” y “ceros” forma parte del conjunto:
0n1n
Los trece quintuplos usados para el diseño de dicha máquina fueron los siguientes:
(0,b,b,6,D)Esta máquina puede considerarse como una máquina con dos salidas, la salida que escribe un símbolo en la cinta, y la salidad que indica el sentido del movimiento de la cabeza lectora. Ignoremos momentáneamente el quinto componente del quintuplo. Esto nos deja lo siguiente:
(0,0,X,1,D)
(1,0,0,1,D)
(1,1,1,1,D)
(1,X,X,2,I)
(1,b,b,2,I)
(2,1,X,3,I)
(3,1,1,3,I)
(3,0,0,4,I)
(3,X,X,5,D)
(4,0,0,4,I)
(4,X,X,0,D)
(5,X,X,6,D)
(0,b,b,6)Esto se parece harto a las máquinas de estado finito que vimos en la entrada anterior, en las cuales estando la máquina en cierto estado (lo que vendría siendo arriba el primer componente de cuadruplo) y recibiendo la máquina cierta entrada (el segundo componente del cuadruplo), el siguiente estado de la máquina está especificado por el tercer componente del cuadruplo, y la salida producida por la máquina está dada por el cuarto componente del cuadruplo. Con cada cuadruplo podemos construír de inmediato un grafo (en este caso, el grafo de una máquina Mealy) que especifica el comportamiento de la máquina. Restaurando el quinto componente tenemos una máquina con dos salidas en lugar de una sola. Cada quintuplo parece contener la misma información con la cual podríamos construír la tabla de estado o el grafo de estado para una máquina de estados finitos. En efecto, en cualquier quintuplo se especifica que si la máquina está en un cierto estado sk y se le aplica cierta entrada tomada del conjunto {0,1,X,b}, entonces el siguiente estado quedará determinado por completo así como las salidas. Se trataría de una máquina de estados finitos que en vez de tener una salida activa tendría dos salidas activas todo el tiempo, una de ellas especificando el símbolo que será grabado en la cinta por la cabeza lectora, y la otra especificando el sentido del movimiento de la cabeza lectora, ya sea hacia la derecha (D) o hacia la izquierda (I):
(0,0,X,1)
(1,0,0,1)
(1,1,1,1)
(1,X,X,2)
(1,b,b,2)
(2,1,X,3)
(3,1,1,3)
(3,0,0,4)
(3,X,X,5)
(4,0,0,4)
(4,X,X,0)
(5,X,X,6)
La tabla de estado de esta máquina es la que se muestra a continuación:
| Entradas | Salidas | ||||||||
| Estado actual |
0 | 1 | X | b | 0 | 1 | X | b | Sentido del movimiento |
| s0 | s6 | 0 | 0 | 0 | 1 | 1 (D) | |||
| s0 | s1 | 0 | 0 | 1 | 0 | 1 (D) | |||
| s1 | s1 | 1 | 0 | 0 | 0 | 1 (D) | |||
| s1 | s1 | 0 | 1 | 0 | 0 | 1 (D) | |||
| s1 | s2 | 0 | 0 | 1 | 0 | 0 (I ) | |||
| s1 | s2 | 0 | 0 | 0 | 1 | 0 (I ) | |||
| s2 | s3 | 0 | 0 | 1 | 0 | 0 (I ) | |||
| s3 | s3 | 0 | 1 | 0 | 0 | 0 (I ) | |||
| s3 | s4 | 1 | 0 | 0 | 0 | 0 (I ) | |||
| s3 | s5 | 0 | 0 | 1 | 0 | 1 (D) | |||
| s4 | s4 | 1 | 0 | 0 | 0 | 0 (I ) | |||
| s4 | s0 | 0 | 0 | 1 | 0 | 1 (D ) | |||
| s5 | s6 | 0 | 0 | 1 | 0 | 1 (D ) | |||
En la construcción de esta tabla de estado, se le ha asignado a un sentido de movimiento de la cabeza lectora hacia la izquierda un valor de “0”, y se le ha asignado a un sentido de movimiento de la cabeza lectora hacia la derecha un valor de “1”:
Sentido del movimiento = 0 (Movimiento hacia la izquierda, I )
Sentido del movimiento = 1 (Movimiento hacia la derecha, D)
En lo que respecta a los símbolos del alfabeto de entrada, podemos hacer una asignación (arbitraria) como la siguiente (con la cual con dos alambres basta para representar cada uno de los cuatro símbolos del alfabeto, en caso de que no queramos usar cuatro alambres, además del alambre adicional que se requiere para indicar el sentido del movimiento de la cabeza lectora en cada quintuplo):
{b,0,1,X} = {00,01,10,11}
Usando una tablilla para proyectos electrónicos, varios circuitos integrados y alambrado de cobre para interconexión de los componentes (compuertas lógicas y flip-flops), podemos construír sin mayores problemas una máquina de estados finitos que produzca la tabla de estado anterior. Esto podría crear la ilusión de que podemos emular una máquina Turing con una máquina de estados finitos. Sin embargo, no es así, ya que el truco está en que la información en la cinta -que es parte integral de la máquina Turing- puede ser alterada borrando cualquier símbolo en la cinta reemplazándolo por otro símbolo, algo que no puede hacer una máquina de estados finitos; esto además de que la máquina Turing no tiene un “tope” de memoria máxima sino que se cuenta con toda la memoria que se requiera para la tarea que sea.
Al sacar los quintuplos de la unidad secuencial de la máquina Turing:
para moverlos poniéndolos en la cinta:
no sólo estamos disminuyendo la cantidad de componentes electrónicos y alambrado que había en la unidad secuencial. La lógica de secuenciación que antes era inalterable se vuelve moldeable por estar puesta en la misma cinta. Y en lugar de tener que volver a reinterconectar todos los circuitos agregando quizá más componentes integrados para tener otra máquina distinta que sólo puede responder a otro conjunto pre-especificado de quintuplos, tenemos algo en lo que todo lo que se requiere es poner en la cinta un nuevo conjunto de quintuplos cada vez que se vaya a requerir para solucionar un problema diferente. La memoria en la unidad de estados finitos de la máquina Turing (pegada a la cabeza lectora) es una memoria fija, inalterable, es lo que en jerga técnica se conoce como firmware, mientras que la memoria en la cinta es una memoria alterable a costo mínimo; y aunque al principio pueda ser algo cara, a la larga resulta muchísimo más económica. En nuestra visión contemporánea, podemos visualizar la memoria de la cinta como el equivalente de una memoria RAM, mientras que la memoria en la unidad de estados finitos pegada a la cabeza lectora es una memoria de lectura únicamente (ROM) complementada con circuitos de control para poder llevar a cabo las secuenciaciones básicas. Lo que se ha hecho al mover los quintuplos hacia la cinta, convirtiendo a la máquina Turing T en una máquina Turing universal U, es esencialmente lo mismo que lo que hizo John von Neumann al proponer que los programas de cómputo fuesen movidos y puestos en la misma memoria RAM de la computadora electrónica junto con los datos a ser manipulados por el programa, convirtiendo a las computadoras en máquinas de cómputo multi-usos sumamente versátiles, con lo cual la misma máquina que se usa para el modelaje de algún problema científico como el pronóstico del tiempo se puede usar también como un procesador de palabras (documentos) o como una reproductora de archivos musicales. Tal es la trascendencia de una idea tan sencilla que hoy conocemos como la arquitectura de von Neumann. En las ciencias computacionales, la idea resulta equiparable al descubrimiento del cero. Lo sorprendente es que la máquina Turing fuese concebida décadas antes de que se contara con la tecnología requerida para miniaturizar circuitos integrados en gran escala, décadas antes de que se inventaran las memorias de acceso aleatorio RAM.
Existen otras formulaciones de la máquina Turing que hemos estudiado aquí. Una de ellas permite que la cinta contenga no una sino dos o más pistas diferentes, de modo tal que la máquina pueda leer más de un símbolo a la vez (y de hecho esta es la manera en la que operan muchos diseños de computadoras que pueden leer y escribir en ocho pistas diferentes a la vez, o sea máquinas capaces de poder leer y escribir un byte de información a la vez usando el bit que pueden manipular en cada una de las ocho pistas). Otro diseño permite que haya varias unidades procesadoras de estado finito operando independientemente sobre pistas distintas. Inclusive, en vez de tener tantas opciones, podemos requerir que a la máquina Turing le sea permitido manipular únicamente dos símbolos, el símbolo de un espacio en blanco “b” y un símbolo adicional. Todas estas definiciones alternas son equivalentes la una a la otra en el sentido de que para una máquina Turing siempre es posible encontrar otra que pueda efectuar la misma tarea.
Cualquier computadora digital, sin importar lo grande y poderosa que sea, está determinada por el estado actual en que se encuentran todos los bits que hay en el acumulador de la unidad de procesamiento central, en su “pila”, en sus registros internos, en su memoria RAM, en todo lo que pueda almacenar la computadora como “ceros” y “unos”. El número posible de combinaciones de “ceros” y “unos” que determina el estado de una computadora puede ser astronómicamente grande, pero ciertamente no es infinitamente grande, y una vez prefijado dicho estado determinará fatalmente el estado siguiente de la máquina, y el estado siguiente, y el estado siguiente, y así sucesivamente (a menos de que haya intervenciones por parte del usuario alterando el estado de la máquina). En efecto, cualquier computadora puede ser reducida conceptualmente a una máquina Turing. Lo cual implica que el problema matemático-lógico que podamos resolver en una computadora también lo podemos resolver con cualquier otra computadora, siempre y cuando tengamos recursos ilimitados de memoria para emprender la tarea. Lo que importa en todo caso es el conjunto de instrucciones en lenguaje de máquina con el que contemos en cada máquina. Podemos, en principio, diseñar un programa de emulación que una vez instalado en una máquina que funciona bajo el sistema operativo UNIX dará toda la apariencia de que se trata de una máquina en la cual está instalado un sistema operativo Mac OS X. La única pista que podrá tener el usuario de que está siendo engañado por un programa impostor será en todo caso la disminución en la velocidad de procesamiento que puede verse disminuída en una forma que puede ser detectable, pero si el procesador es lo suficientemente rápido no habrá manera en que el usuario pueda saber lo que está ocurriendo realmente detrás de la fachada gráfica que la máquina le está presentando.