Para quedar satisfecho de que la máquina que no puede ver en efecto es una máquina original IBM PC AT, el individuo empieza utilizando la ventana de comandos de línea, escribiendo primero la fecha actual (algo que siempre pedía el sistema operativo PC DOS a los usuarios antes de mostrar el “prompt”) así como el tiempo actual, apareciendo la ventana siguiente (se recomienda en esta imagen y las que siguen ampliarlas para poder apreciar mejor los detalles):
Hecho esto, haciendo el cambio del drive A al drive C y al directorio WINDOWS en donde se encuentra el programa ejecutable win.exe, echando a andar la interfaz gráfica de Windows 1.01 el usuario abre dicha interfaz gráfica apareciendo la ventana típica de apertura de Windows 1.01 (ampiar imagen para mayor detalle):
Una vez estando dentro del entorno de la interfaz gráfica de Windows 1.01, nuestro personaje abre el programa MSDOS.EXE a través de la interfaz gráfica Windows 1.01, en donde le pide al programa MS-DOS Executive de Windows 1.01 mostrarle el contenido del drive A:
En efecto, allí están todos los programas típicos que venían incluídos con el sistema operativo PC DOS. Usando el Mouse, el usuario hace el cambio del drive A al drive C que es el disco duro, para ver los contenidos del disco duro:
Entre los programas que hay allí, podemos ver que se encuentra el procesador de palabras WRITE.EXE de Windows 1.01, el cual decide echar a andar este editor de texto Microsoft Write:
Nuestro invitado decide cerrar el programa editor de texto y decide echar a andar el programa PAINT.EXE, el cual es el primer antecesor de todos los demás programas Paint incluídos por Microsoft como parte de todos sus sistemas operativos:
Habiendo echado a andar el programa PAINT.EXE, nuestro personaje decide poner a prueba dicho procesador de gráficos trazando una elipse y poniendo algo de texto en una parecida a como se muestra a continuación, en el conocimiento de que todo esto se está llevando a cabo bajo la interfaz gráfica Windows 1.01:
Habiendo hecho lo anterior, decide cerrar el programa PAINT.EXE y abrir a continuación el Bloc de Notas de Windows 1.01 en donde se anima a escribir algo de texto:
Satisfecho de que el Bloc de Notas de Windows 1.01 (el primer Bloc de Notas elaborado por Microsoft) está funcionando, decide cerrarlo para abrir la Calculadora de Windows 1.01 echando a andar el programa CALC.EXE:
Satisfecho de que la calculadora funciona como debe ser, cierra el programa CALC.EXE y abre el Panel de Control de la interfaz gráfica Windows 1.01 (que como puede verse, es algo muy crudo y primitivo con funciones de modificación muy limitadas en comparación con lo que puede ser modificado con el Panel de Control de un sistema operativo como Windows XP o como Windows 8.1):
Una vez que nuestro personaje ha hecho todas las pruebas anteriores, declara que la máquina es, en efecto, una PC IBM original con el sistema operativo PC DOS instalado en ella así como la interfaz gráfica Windows 1.01 instalada en el directorio WINDOWS del disco duro. Sin embargo, una vez que nuestro invitado ha dado su veredicto, se le asegura que la máquina no es una IBM PC original de esos tiempos; es más, ni siquiera es una máquina actual que tenga instalado el sistema operativo DOS o que tenga instalado sistema operativo alguno de Microsoft. Se trata de una computadora Macintosh funcionando con el sistema operativo Mac OS X. Pero en la simulación de todo lo anterior, la máquina ni siquiera usó un programa ejecutable instalado en ella, bajó un programa de la Web que funciona bajo código JavaScript y algo de Java. Para convencerlo, se le muestra la ventana completa del DOS en donde puede apreciar en la parte inferior las funciones adicionales agregadas a la simulación que ciertamente no eran parte del sistema operativo original PC DOS:
Hecho lo anterior, con la simulación del DOS se hace el cambio simulado del drive A al disco duro C con el comando usual DOS, estando presente en todo tiempo la interfaz completa:
y se hace también el examen simulado del directorio C WINDOWS con el comando DOS dir:
y nuevamente en la simulación de Windows 1.01 se abre una ventana dual (algo que se podía hacer en aquél entonces):
De este modo, nuestro invitado se queda estupefacto con la boca abierta. Una máquina contemporánea que no tenía ningún sistema operativo DOS instalado en ella ha sido capaz de emular a la perfección todo lo que hacía una computadora IBM PC original.
La realidad de una simulación como la anterior no es una invención. De hecho, las capturas de imagen que se han presentado fueron obtenidas con una simulación de Windows 1.01 y del sistema operativo PC DOS bajo el título “This Emulator Runs Windows 1.01 in Your Browser” publicada por Jon Russell en el sitio Web thenextweb.com, reproduciendo un emulador del sistema operativo Windows 1.01 desarrollado por Jeff Par. De acuerdo a su autor, la simulación del emulador del sistema operativo Windows 1.01 fue configurada para una máquina simulada con una velocidad de reloj de 4.77 MHz (era a lo que corrían la mayoría de las computadoras de escritorio de ese entonces) con 256 Kb de memoria RAM y un monitor de colores CGA (predecesor del monitor de colores VGA que a su vez fue el predecesor del SVGA que a su vez fue el predecesor de los monitores de pantalla plana de la actualidad), usando el modelo original IBM PC XT 5160 con el tipo de fuentes (para la impresión de caracteres en la pantalla) CGA, simulando también un disco duro de 10 Mb con Windows 1.01 pre-instalado, haciéndose la aclaración de que la emulación no guardará ningún tipo de cambio simulado bajo ese Windows 1.01 al salir del navegador en virtud de haber sido pre-configurado para empezar siempre con Windows 1.01 en el mismo estado, y agregando también que el indicador del Mouse puede ser controlado con el Mouse verdadero de la máquina actual pero solo cuando el Mouse está dentro de la ventana “CGA Display” de la simulación, siendo esta una restricción impuesta por el navegador y no por la computadora en sí.
En el mismo sitio se pone a disposición de los lectores otra simulación, la simulación de Windows 3.1, elaborada por James Friend, cuya captura de imagen se muestra a continuación:
Y nuevamente, lo que está siendo ejecutado y presentado no es una interfaz gráfica Windows 3.1 original (Windows 3.1 todavía no llegaba al status de sistema operativo), se trata de una emulación. enviada a través de Internet para ser usada de inmediato sin necesidad de tener que descargar ningún programa ejecutable, todo se lleva a cabo a través del navegador.
Lo importante es que, en principio, siempre y cuando se cuente con una memoria lo suficientemente grande y con un mínimo estipulado de requisitos de hardware, podemos usar cualquier máquina para simular el comportamiento de cualquier otra, lo cual al ser enunciado como un postulado a ser demostrado es indicativo de que todas las computadoras son equivalentes a una misma máquina universal mínima de la cual pueden ser derivadas. Esto parece ser algo bastante amplio y bastante pesado, y se vuelve necesario irlo digiriendo poco a poco.
En esta entrada haremos una disgresión para repasar el caso de una máquina históricamente muy especial, una máquina propuesta por el matemático inglés Alan Turing en 1936, la cual es el punto de partida para deducciones teóricas de gran importancia que tienen que ver con lo que se entiende teóricamente por computabilidad así como lo que es posible y no es posible esperar resolver con una computadora digital del tipo que sea.
Esencialmente, una máquina Turing consiste de una máquina de estado-finito y una cinta que está dividida en celdas; cada celda puede contener a lo más un símbolo tomado de un alfabeto finito de caracteres que al principio contendrá únicamente el conjunto de símbolos {0,1} pero que se puede ir ampliando conforme sea necesario. Utilizamos el símbolo especial b para representar una celda en blanco que no contiene ninguna información. En cualquier instante, sólo hay un número finito de celdas en la cinta que no son celdas en blanco. La máquina de estado-finito tiene un cabezal mediante el cual puede puede leer el contenido de cada celda y puede también imprimir un símbolo nuevo en cada celda borrando el símbolo que había previamente en dicha celda. De este modo, podemos conceptualizar una máquina Turing del modo siguiente:
La cabeza de lectura y escritura (puede llevar a cabo ambas funciones, y por lo tanto es una unidad de entrada y salida) de la máquina se puede mover únicamente hacia la derecha o hacia la izquierda. Al igual que como ocurre con cualquier otra computadora digital, la máquina Turing es alimentada con pulsos de reloj que hacen que la máquina pase de un estado a otro con cada pulso de reloj. Después de recibir un pulso de reloj, dependiendo de su estado presente, la unidad puede no hacer nada (detenerse), o puede completar tres acciones. Estas acciones son: (1) imprimir en la celda que está siendo leída un símbolo tomado del alfabeto (puede ser el mismo símbolo que ya estaba allí), (2) pasar al siguiente estado (puede ser el mismo estado previo), y (3) mover la cabeza de lectura-escritura una celda hacia la izquierda o hacia la derecha.
Podemos describir la acción de cualquier máquina Turing mediante una serie de quintuplos de la forma:
{s,i,i’,s’,d}
en donde s representa el estado actual de la máquina. i representa el símbolo que está siendo leído por el cabezal, i’ representa el símbolo que se imprime en la celda, s’ representa el siguiente estado (el estado nuevo), y d representa la dirección hacia la cual se mueve el cabezal (hacia la izquierda, I, o hacia la derecha, D).
El siguiente ejemplo ilustra mejor la acción ordenada por un quintuplo en una máquina Turing:
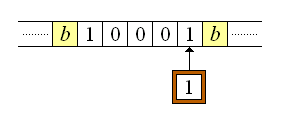
Supóngase que se tiene una máquina Turing para la cual es válido el quintuplo anterior, la cual se encuentra en la siguiente configuración:
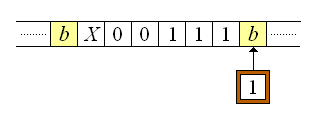
Después del pulso de reloj que hace que la máquina pase de un estado al siguiente, de acuerdo al quintuplo la nueva configuración de la máquina será la siguiente:
En pocas palabras, si el estado actual de la máquina es 2, y el símbolo que está siendo leído es 1, entonces de acuerdo al quintuplo se imprime en la celda un 0, el estado de la máquina para de 2 a 1, y la cabeza de lectura-escritura de la máquina se mueve una posición hacia la derecha posicionándose en la celda contigua. Podemos mostrar mejor la acción mediante el siguiente gráfico animado:
Obviamente, se requiere más de un quintuplo para describir una máquina Turing, y de hecho se pueden requerir muchos quintuplos. Es indispensable también que no haya en el conjunto de quintuplos dos quintuplos distintos que empiecen con el mismo estado s y el mismo símbolo i en la celda. Esto se requiere para que la máquina Turing sea una máquina determinística (de lo contrario, la máquina Turing no sabría cuál de los dos quintuplos seleccionar para llevar a cabo la siguiente acción). De este modo, la acción de una máquina Turing está completamente especificada por el estado actual de la máquina de estado-finito y el símbolo que está siendo leído. Si una máquina Turing entra en una configuración en la cual su estado actual y el símbolo que está siendo leído no forman parte del conjunto de quintuplos, la máquina Turing se detiene.
Tal y como ocurre con las máquinas de estado-finito ordinarias, especificamos un estado de inicio, simbolizado como 0, en el cual la máquina comienza a efectuar cualquier cálculo. Suponemos también una configuración inicial para la cabeza de lectura-escritura en la cual la cabeza de lectura-escritura está posicionada en el símbolo más a la izquierda en la cinta que no sea una celda en blanco. Si toda la cinta está inicialmente en blanco, entonces la cabeza de lectura-escritura puede estar posicionada al inicio en cualquier parte de la cinta.
PROBLEMA: Si una máquina Turing está definida mediante el siguiente conjunto de quintuplos:
descríbase lo que ocurre cuando se empieza con la máquina en la siguiente configuración:
Consultando el conjunto de quintuplos, vemos que el quintuplo que describe lo que sucede al aplicar el primer pulso de reloj a ésta máquina Turing es el quintuplo (0,0,1,0,D). En pocas palabras, se imprime un 1 en la celda (borrando el 0 que había), la máquina de estado-finito permanece en su estado 0, y la cabeza de lectura-escritura se mueve hacia la derecha. La nueva configuración es entonces:
En esta configuración, puesto que el estado de la máquina es 0 y el símbolo que está siendo leído es 1, el quintuplo que describe lo que ocurre al aplicar el siguiente pulso de reloj a la máquina Turing es el quintuplo (0,1,0,0,D). En pocas palabras, se imprime un 0 (borrando el 1 que había), la máquina de estado finito permanece en estado 0, y la cabeza de lectura-escritura se mueve hacia la derecha. La nueva configuración es entonces:
De éste modo, vemos que la máquina va pasando por las siguientes configuraciones restantes:
Podemos mostrar mejor la acción de esta máquina Turing mediante el siguiente gráfico animado:
A continuación, veremos una aplicación elemental de las máquinas Turing que ilustran sus capacidades de reconocimiento. Para ello, definiremos formalmente un estado final de una máquina Turing como un estado que no es el primer símbolo de ningún quintuplo. De este modo, al entrar en un estado final, la máquina Turing se detiene sin importar cuál sea el símbolo que está siendo leído por la cabeza de lectura-escritura.
Considérese ahora el siguiente conjunto de quintuplos que describen una máquina Turing un poco más elaborada:
Obsérvese que al alfabeto de símbolos propios de la cinta, se le ha agregado un símbolo especial que llamaremos X, de modo tal que el alfabeto de la cinta es ahora {0,1,X}, constando de tres elementos.
Aunque no parezca obvio a primera vista, una máquina Turing definida con el anterior conjunto de quintuplos es capaz de poder reconocer hileras de símbolos en la cinta de la forma: 0n1n siendo n un entero positivo. Puesto de otro modo, la máquina Turing puede reconocer las siguientes hileras de caracteres en la cinta, deteniéndose una vez que ha terminado de llevar a cabo sus labores de reconocimiento:
01
0011
000111
00001111
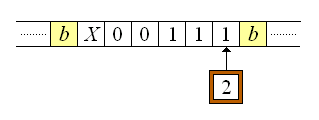
La siguiente cinta tiene precisamente una hilera de caracteres que cumple con esta condición antes de empezar el procesamiento Turing sobre la información que contiene la cinta:
Para el inicio, tal y como lo hemos acordado, colocaremos el cabezal lo más a la izquierda que se pueda en el primer lugar donde no haya una celda en blanco:
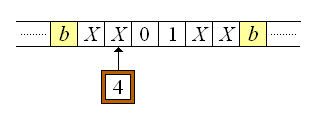
Estando la máquina inicialmente en el estado 0 y siendo el símbolo leído en la cinta 0, el quintuplo que entra en acción es (0,0,X,1,D), borrándose el 0 e imprimiéndose una X en la celda tras lo cual la máquina entra al estado 1 y el cabezal se mueve hacia la derecha. De este modo, podemos describir la configuración posterior inmediata de la máquina del modo siguiente:
A continuación se llevará a cabo un análisis detallado paso-a-paso sobre lo que va ocurriendo cuando la máquina Turing que comienza en la configuración mostrada al principio va ejecutando cada una de las instrucciones ordenadas por el quintuplo que corresponda ejecutar. Si inicialmente la máquina está en el estado “0” y la cabeza de lectura-escritura está leyendo un “0” en la cinta, entonces el quintuplo que es invocado es el quintuplo (0,0,X,1,D), el cual hace que la cabeza de lectura-escritura de la máquina borre el “0” de la cinta poniendo una “X” en su lugar, pasando al estado “1”, y moviéndose la cabeza de lectura-escritura una posición hacia la derecha. Se irá mostrando gráficamente el aspecto de la máquina correspondiente a cada quintuplo que estará siendo invocado, a partir de la configuración inicial:
(0,0,X,1,D):
Configuración inicial. La cabeza lectora se moverá una posición hacia la derecha después de haberse imprimido una “X” en la cinta, y el estado de la máquina cambiará de su estado inicial “0” para pasar al estado “1”.
(1,0,0,1,D):
Esta es la configuración que sigue. La cabeza lectora se ha movido una posición hacia la derecha después de haber imprimido una “X” en la cinta borrando el “0” que tenía en dicha posición.
(1,0,0,1,D):
La tercera configuración. La cinta continuará moviéndose hacia la derecha.
(1,1,1,1,D):
La cuarta configuración. La máquina sigue en el estado “1” pero ahora está leyendo un “1” y no un “0”. No importa, porque de cualquier modo se seguirá moviendo hacia la derecha, una posición a la vez. El valor “1” que la cabeza lectora estaba leyendo en la cinta permanece en efecto inalterado, porque el quintuplo especifica que se imprima un “1” en donde ya hay un “1”, lo cual en efecto implica dejar las cosas igual que como están mientras la cabeza lectora se mueve hacia la derecha.
(1,1,1,1,D):
La quinta configuración. La máquina sigue en el estado “1” y ahora está leyendo un “1”. Nuevamente, esto en efecto implica dejar las cosas igual que como están mientras la cabeza lectora se mueve otra vez hacia la derecha.
(1,1,1,1,D):
La sexta configuración. La máquina sigue en el estado “1” y ahora está leyendo un “1”. Nuevamente, esto en efecto implica dejar las cosas igual que como están mientras la cabeza lectora se mueve otra vez hacia la derecha.
(1,b,b,2,I):
La séptima configuración. La máquina sigue en el estado “1”, pero ahora está leyendo un espacio en blanco “b”. Esto hará que la cabeza lectora invierta el sentido de su movimiento, moviéndose de derecha a izquierda en vez de continuar moviéndose hacia la derecha, a la vez que el estado de la máquina Turing deberá cambiar de “1” a “2”.
(2,1,X,3,I):
La octava configuración. El estado de la máquina ha cambiado de “1” a “2”, pero al estar la máquina en dicho estado y al estar leyendo la cabeza lectora un “1”, la máquina Turing está predestinada (de acuerdo al conjunto de quintuplos) a cambiar de estado y a continuar moviéndose hacia la izquierda.
(3,1,1,3,I):
La novena configuración. El estado de la máquina ha cambiado de “2” a “3”, y al estar leyendo la cabeza lectora un “1” esto hará que la cabeza lectora se mueva hacia la izquierda sin cambiar el contenido de la cinta y sin cambiar el estado de la máquina.
(3,1,1,3,I):
La décima configuración. El estado de la máquina sigue siendo “3”, y al estar leyendo la cabeza lectora un “1” en su nueva posición, la cabeza lectora se moverá hacia la izquierda sin cambiar el contenido de la cinta y sin cambiar el estado de la máquina.
(3,0,0,4,I):
La décimoprimera configuración. El estado de la máquina sigue siendo “3” pero deberá cambiar a “4” al estar leyendo la cabeza lectora un “0” en lugar de un “1”, lo cual invoca el quintuplo que hará que ocurran dichos cambios. La cabeza lectora continuará moviéndose hacia la izquierda pero sin cambiar el contenido de la cinta.
(4,0,0,4,I):
La décimosegunda configuración. El estado de la máquina ha cambiado de “3” a “4”. La cabeza lectora dejará intacto en la cinta el “0” que estaba leyendo, moviéndose una posición hacia la izquierda.
(4,X,X,0,D):
La treceava configuración. La máquina se ha topado con el símbolo “X” que había puesto al partir de la configuración inicial. La cabeza lectora ha encontrado el extremo izquierdo de la hilera de ceros y unos en la cinta, y empezará nuevamente con un movimiento de “barrido” de izquierda a derecha. Obsérvese que el estado de la máquina es “reseteado” desde “4” hasta “0” para comenzar de nuevo repitiendo un proceso como el que se llevó a cabo en la ejecución de las doce instrucciones previas.
(0,0,X,1,D):
La catorceava configuración. Esto es idéntico a lo que ocurrió cuando se partió de la configuración inicial. La cabeza lectora se moverá una posición hacia la derecha después de haberse imprimido una “X” en la cinta, y el estado de la máquina cambiará de su estado inicial “0” para pasar al estado “1”.
(1,0,0,1,D):
La quinceava configuración. La cabeza lectora se ha movido una posición hacia la derecha después de haber imprimido una “X” en la cinta borrando el “0” que tenía en dicha posición. Obsérvese que se han eliminado ya los dos “0” que había en el extremo izquierdo de la cinta, y podemos sospechar que la siguiente secuencia de eventos será para ir borrando los “1” que se encuentran en el extremo derecho de la cinta.
(1,1,1,1,D):
La dieciseisava configuración. La cinta continuará moviéndose hacia la derecha. La máquina sigue en el estado “1” pero ahora está leyendo un “1” y no un “0”. No importa, porque de cualquier modo se seguirá moviendo hacia la derecha, una posición a la vez. El valor “1” que la cabeza lectora estaba leyendo en la cinta permanece en efecto inalterado, porque el quintuplo especifica que se imprima un “1” en donde ya hay un “1”, lo cual en efecto implica dejar las cosas igual que como están mientras la cabeza lectora se mueve hacia la derecha.
(1,1,1,1,D):
La diecisieteava configuración. La máquina sigue en el estado “1” y ahora está leyendo un “1”. Nuevamente, esto en efecto implica dejar las cosas igual que como están mientras la cabeza lectora se mueve otra vez una posición hacia la derecha.
(1,X,X,2,I):
La dieciochoava configuración. La cabeza lectora de la máquina se ha encontrado por primera vez con un símbolo “X” en el extremo derecho de la cinta, el mismo símbolo que puso al llevarse a cabo el ciclo de “barrido” anterior. El símbolo “X” permanecerá intacto, pero el estado de la máquina cambiará de “1” a “2”, y el sentido de movimiento de la cabeza lectora se invertirá, moviéndose de derecha a izquierda en vez de continuar moviéndose hacia la derecha, a la vez que el estado de la máquina Turing deberá cambiar de “1” a “2” al igual que como sucedió en el ciclo anterior.
(2,1,X,3,I):
La décimonovena configuración. El estado de la máquina ha cambiado de “1” a “2”, pero al estar la máquina en dicho estado y al estar leyendo la cabeza lectora un “1”, la máquina Turing está predestinada (de acuerdo al conjunto de quintuplos) a cambiar de estado y a continuar moviéndose hacia la izquierda.
(3,1,1,3,I):
La vigésima configuración. El estado de la máquina ha cambiado de “2” a “3”, y al estar leyendo la cabeza lectora un “1” esto hará que la cabeza lectora se mueva hacia la izquierda sin cambiar el contenido de la cinta y sin cambiar el estado de la máquina.
(3,0,0,4,I):
La vigésimoprimera configuración. El estado de la máquina sigue siendo “3” pero deberá cambiar a “4” al estar leyendo la cabeza lectora un “0” en lugar de un “1”, lo cual invoca el quintuplo que hará que ocurran dichos cambios. La cabeza lectora continuará moviéndose hacia la izquierda pero sin cambiar el contenido de la cinta.
(4,X,X,0,D):
La vigésimosegunda configuración. La máquina se ha topado con el segundo símbolo “X” que había puesto en el extremo izquierdo de la cinta. La cabeza lectora ha llegado así al extremo izquierdo de la hilera de ceros y unos en la cinta que están acotado por símbolos “X”, y empezará nuevamente con un movimiento de “barrido” de izquierda a derecha. Obsérvese que el estado de la máquina es “reseteado” desde “4” hasta “0” para comenzar de nuevo repitiendo otro ciclo como el que se llevó a cabo en la ejecución de las instrucciones previas.
(0,0,X,1,D):
La vigésimotercera configuración. La cabeza lectora se moverá una posición hacia la derecha después de haberse imprimido una “X” en la cinta, y el estado de la máquina cambiará de su estado inicial “0” para pasar al estado “1”.
(1,1,1,1,D):
La vigésimocuarta configuración. La máquina ha cambiado del estado “0” al estado “1” y ahora está leyendo un “1”. Esto en efecto implicará dejar las cosas igual que como están mientras la cabeza lectora se mueve otra vez una posición hacia la derecha. Obsérvese que en este punto ya no queda ningún “0” en la cinta, sólo queda un “1”, acotado por tres símbolos “X” a la izquierda y por dos símbolos “X”. En este punto, resulta claro por la manera en que están especificados los quintuplos de la máquina Turing que no se le permitirá a la cabeza lectora movimiento alguno a lo largo de una hilera de símbolos “X” ni de izquierda a derecha ni de derecha a izquierda.
(1,X,X,2,I):
La vigésimoquinta configuración. La cabeza lectora de la máquina se ha encontrado por de nueva cuenta con un símbolo “X” en el extremo derecho de la cinta al estarse moviendo de izquierda a derecha, el mismo símbolo que puso al llevarse a cabo el ciclo de “barrido” anterior. El símbolo “X” permanecerá intacto, pero el estado de la máquina cambiará de “1” a “2”, y el sentido de movimiento de la cabeza lectora se invertirá, moviéndose de derecha a izquierda en vez de continuar moviéndose hacia la derecha, a la vez que el estado de la máquina Turing deberá cambiar de “1” a “2” al igual que como sucedió en el ciclo anterior.
(2,1,X,3,I):
La vigésimosexta configuración. El estado de la máquina ha cambiado de “1” a “2”, pero al estar la máquina en dicho estado y al estar leyendo la cabeza lectora un “1”, la máquina Turing está predestinada (de acuerdo al conjunto de quintuplos) a cambiar de estado de “2” a “3” y a continuar moviéndose hacia la izquierda. Obsérvese que al imprimir la cabeza lectora de la máquina Turing un símbolo “X” en donde había un “1”, se han agotado los “0” y los “1” que había en la cinta, habiendo ya únicamente símbolos “X”. Podemos intuír que los en el conjunto de quintuplos habrá instrucciones que llevarán a la máquina a un estado final en el cual quedará detenida.
(3,X,X,5,D):
La vigésimoséptima configuración. La cabeza lectora de la máquina se ha movido una posición hacia la izquierda en donde se encuentra con otro símbolo “X”. Siendo su estado el estado “3”, el quintuplo que determina la acción subsecuente ordena que la máquina habrá de cambiar a un estado en el que no había estado previamente, el estado “5”, y ordena también que el sentido de movimiento de la cabeza lectora habrá de cambiar de sentido, llevándose a cabo de izquierda a derecha en vez de llevarse a cabo de derecha a izquierda.
(5,X,X,6,D):
La vigésimoctava configuración. La cabeza lectora de la máquina se ha movido una posición hacia la derecha habiendo invertido el sentido de su movimiento, y el estado de la máquina ha cambiado de “3” a “5”. Al estar leyendo un símbolo “X” y estando en el estado “5”, la máquina deberá continuar moviéndose una posición hacia la derecha pasando al estado “6”.
De este modo, la máquina habrá llegado a la siguiente configuración:
Pero al no haber ningún quintuplo que especifique la acción que deberá tomar la máquina una vez que se encuentre en el estado “6” sin importar el símbolo que esté leyendo la cabeza lectora, la máquina se detiene. La máquina Turing, en efecto, ha llegado a su estado final, que en este caso es el estado “6”.
Así pues, la máquina se detiene en el estado 6, el único estado final. Obsérvese que al final, todos los símbolos 0 y 1 en la cinta han sido reemplazados por una hilera de símbolos X.
Podemos mostrar y comprender mejor la acción de esta máquina Turing mediante el siguiente gráfico animado dado en “cámara lenta”:
A continuación tenemos el mismo gráfico animado pero a una velocidad mayor una vez que las acciones que ocurren en el gráfico animado anterior han sido entendidas:
La forma en la que opera la máquina es conceptualmente sencilla. La cabeza lectora pone primero una “tacha” (una X) en el “cero” que está más a la izquierda en la cinta, y hecho esto la cabeza lectora se va desplazando hacia la derecha hasta encontrar el “1” que está en el extremo derecho para “tacharlo”, tras lo cual la cabeza lectora se regresa para buscar el siguiente “cero” con el fin de “tacharlo”. Por cada “cero” que es “tachado” en la cinta se “tacha” un “1”, hasta que se hayan agotado en cantidades iguales los “ceros” y los “unos”. Si sobra un “0” o sobra un “1”, entonces la máquina no termina en el estado final de aceptación de la hilera (el estado 6). Hay quintuplos que actúan como equipo con un propósito similar. Con el par de quintuplos (1,0,0,1,D) y (1,1,1,1,D), la cabeza lectora se va desplazando constantemente hacia la derecha pasando por encima de los “ceros” y los “unos” sin cambiar de estado y sin cambiar nada en la cinta, hasta encontrar la primera “X” con la que la máquina cambia del estado 1 al estado 2 (invirtiéndose el sentido del movimiento de la cabeza lectora) bajo el quintuplo (1,X,X,2,I), o hasta encontrar el primer espacio en blanco “b” con el que la máquina también cambia del estado 1 al estado 2 (invirtiéndose también el sentido del movimiento de la cabeza lectora). Por otro lado, el quintuplo (4,X,X,0,D) “resetea” la máquina al estado 0 después de que la cabeza lectora ha llegado al extremo izquierdo de la cinta al leer una “X”.
Al haber llegado a su estado final, la máquina Turing ha reconocido la hilera de ceros y unos que forman parte de la hilera “000111” al haberlos reemplazados por símbolos de borrado “X” y al haberse detenido sin continuar con ninguna otra acción posterior. El lector puede hacer la prueba por sí mismo, si así lo desea, que el mismo quintuplo que especifica esta máquina Turing puede reconocer las siguientes hileras:
00001111
0000011111
000000111111
descritas por la fórmula:
0n1n
Formalizando esto último, la máquina Turing que se ha especificado aquí puede reconocer las hileras que forman parte del siguiente conjunto C (usaremos notación propia de la Teoría de Conjuntos para darle un poco de mayor seriedad al asunto):
C = { 0n1n | n ≥ 0}
El lector puede comprobar también que esta máquina Turing no reconocerá hileras de ceros y unos que no formen parte del conjunto anterior, pudiendo ocurrir en tal caso dos cosas:
1) La máquina entra en un bucle perpetuo sin detenerse jamás.
2) La máquina se detiene, pero sin llegar al estado final de aceptación de la hilera binaria, que en este caso es el estado “6”
PROBLEMA: Para la máquina Turing anterior, descríbase la configuración final de la máquina después de que ésta haya procesado las siguientes cintas:
En los tres casos supondremos que la cabeza lectora de la máquina empieza su procesamiento con la cabeza lectora posicionada en el primer “0” que está en el izquierdo extremo de la cinta, y supondremos que al comenzar se encuentra en el estado de inicio “0”.
En el primer caso, recurriendo al conjunto de quintuplos y empezando con el cabezal de lectura-escritura situado a la posición más a la izquierda en cada caso, encontramos que en la hilera b00111b la máquina se detiene en la siguiente configuración la máquina se detiene sin aceptar la hilera al no haber llegado al estado final “6” (obsérvese que en el conjunto de quintuplos no hay un quintuplo que especifique la acción subsecuente que se deberá tomar si la máquina se encuentra en el estado “5” y la cabeza lectora está leyendo un símbolo “1”):
En el segundo caso, la máquina también se detiene sin aceptar la hilera al no haber llegado tampoco al estado final “6” (obsérvese que en el conjunto de quintuplos no hay un quintuplo que especifique la acción subsecuente que se deberá tomar si la máquina se encuentra en el estado “2” y la cabeza lectora está leyendo un símbolo “X”):
Por último, para la hilera b000011b, la máquina se detiene en la siguiente configuración:
Puesto que la máquina no se detuvo en el estado final 6, la máquina no aceptó (no reconoció) la hilera.
Y en el tercer caso, la máquina se detiene sin aceptar la hilera al no haber llegado al estado final “6”. De nueva cuenta, no hay en el conjunto de quintuplos un quintuplo que especifique la acción subsecuente que se deberá tomar si la máquina se encuentra en el estado “2” y la cabeza lectora está leyendo un símbolo “0”.
Así pues, esta máquina Turing es capaz de resolver lo que en esencia puede ser tomado como un problema lógico-matemático, el problema de reconocer aquellas cintas que tengan una cantidad igual de ceros contiguos posicionados a la izquierda de una cantidad igual de unos contiguos posicionados a la derecha. Los casos que hemos visto son triviales, pero si se trata de una cinta que contiene un millón de ceros y lo que parece ser un millón de unos, ciertamente queremos que la labor de reconocimiento la lleve a cabo una máquina en vez de tener que llevarla a cabo nosotros mismos manualmente. Lo asombroso es que no necesitamos un millón de quintuplos para resolver tal problema, basta con el conjunto de quintuplos que se ha definido arriba.
Resolver un problema matemático-lógico implica el poder encontrar un conjunto de quintuplos tal que si dicho conjunto es proporcionado a una máquina Turing, la máquina se detendrá en el estado final que se le ha asignado a la máquina, lo cual equivale a aceptar la hilera de símbolos que se le ha proporcionado. La máquina Turing que hemos visto es capaz de poder leer tres símbolos: “0”, “1” y “X”, los cuales constituyen el alfabeto de la máquina Turing. Pero no hay razón alguna para que nuestro diseño se limite únicamente a estos tres símbolos. El alfabeto puede incluír todos los símbolos del código ASCII. De hecho, por buen tiempo desde que se diseñaron y construyeron las primeras computadoras, la forma de meterle un programa a la memoria RAM de las computadoras era con una cinta en la que había un caracter ASCII tras otro. El alfabeto puede ser tan grande como nosotros queramos que sea, lo único que se requiere es que sea un alfabeto finito, lo cual se dá por hecho en cualquier diseño de cualquier computadora digital.
Otra cosa importante a tomar en cuenta es que, para resolver un problema matemático-lógico, el conjunto de quintuplos requerido para poder resolver el problema no es único, puede haber muchas formas de especificar otros conjuntos de quintuplos diferentes que serán capaces de poder resolver el mismo problema. Sin embargo, es casi seguro que uno de ellos será el que contiene el menor número posible de quintuplos. De este modo, si un programador A especifica un conjunto de 520 quintuplos para la solución de un problema matemático-lógico, otro programador B especifica un conjunto de 478 quintuplos para la solución del mismo problema, y otro programador C especifica un conjunto de 491 quintuplos para la solución del mismo problema, indudablemente el programador B tendrá el mejor programa de los tres, el programa que requerirá el menor tiempo para resolver el problema. Sin embargo, esto no significa que el programa elaborado por el programador B sea el programa mínimo (con el menor conjunto posible de instrucciones) capaz de resolver el problema. Posiblemente tiempo después habrá otro programador que encontrará la manera de poder resolver el mismo problema con solo 200 instrucciones, dejando a los demás con la boca abierta. Y aún así, quedará la duda sobre la posibilidad de que pueda haber otro programa aún más eficiente. Esto refleja directamente lo que ocurre en la vida real, en donde hay muy buenos programadores que pueden “ver” una manera más eficiente de resolver un problema de la cual otros programadores no se habían dado cuenta. Esta es una habilidad que distingue a los programadores profesionales de los programadores novatos, aunque hay que reconocer que a veces se descubren por mera casualidad o accidente formas más eficientes de poder resolver un problema.
El lector puede, si así lo desea, experimentar con otras hileras de símbolos más elaboradas como la siguiente:
y convencerse de que, efectivamente, esta máquina Turing puede reconocer hileras de símbolos con esta característica, y de hecho son las únicas hileras que puede reconocer.
El lector tal vez quiera probar suerte intentando diseñar máquinas Turing que resuelvan lo siguiente:
PROBLEMA: Diseñar una máquina Turing que sea capaz de poder reconocer el conjunto de todas las hileras de símbolos tales que las hileras terminen en 00.
La máquina Turing pedida debe poder reconocer hileras tales como:
111100
11011000
10101100100
Para este problema, podemos usar una máquina Turing que no cambia en lo absoluto ninguno de los símbolos de la cinta y en la cabeza de lectura-escritura siempre se mueve hacia la derecha. Un conjunto de quintuplos que puede llevar a cabo esto es el siguiente:
Si llamamos al estado “3” el estado final, un conjunto de quintuplos que puede llevar a cabo la tarea es el siguiente:
(0,1,1,0,D)Este tipo de procesamiento Turing es típico del reconocimiento de hileras que son lo que se conoce como expresiones regulares. En el caso de las hileras que estamos manejando aquí, la expresión regular que describe el conjunto de hileras es (0v1)*00 en donde el símbolo “v” actúa como el símbolo “o” (OR) de la lógica Boleana. En la notación matemática de las expresiones regulares (0v1)* representa cualquier hilera (incluyendo la hilera vacía) formada por cualquier combinación posible de “unos” y “ceros”. Otros ejemplos de hileras representadas con la notación de expresiones regulares son los siguientes:
(0,0,0,1,D)
(1,0,0,2,D)
(1,1,1,0,D)
(2,0,0,2,D)
(2,1,1,0,D)
(2,b,b,3,D)
0*1(101)* -> Cualquier número de ceros (incluído ninguno) de ceros, seguido de un “uno” solitario, seguido de cualquier número (incluído ninguno) de tríos 101.El punto importante aquí es que una máquina Turing puede hacer la misma tarea que pueda hacer lo que en Teoría de Autómatas se conoce como una máquina de estado finito, esto es, reconocer un conjunto regular. Sin embargo, hay expresiones (hileras) que no son regulares y que no pueden ser reconocidas (aceptadas al llegar a un estado final de aceptación) por máquinas de estado finito. La superioridad de la máquina Turing sobre todas las demás máquinas radica precisamente en que puede ser programada para un propósito específico.
1v0* -> Un “1” sencillo seguido de cualquier número (incluído ninguno) de ceros.
1*0*(0v1)* -> Cualquier número de unos (incluído ninguno) seguido de cualquier número de ceros (incluído ninguno) seguido de cualquier combinación posible de “unos” y “ceros” (incluyendo la hilera vacía).
PROBLEMA: Diseñar una máquina Turing que sea capaz de reconocer el conjunto de todas las hileras tales que estén descritas por la fórmula:
{ 0n12n | n ≥ 0}
Este problema es parecido al que vimos arriba en el cual el objetivo de la máquina Turing era poder reconocer hileras que forman parte del conjunto:
{ 0n1n | n ≥ 0}
Lo que se requiere ahora en este problema es poder reconocer hileras tales como:
011
001111
000111111
000011111111
Obsérvese el parecido de los conjuntos de hileras a ser reconocidos en este problema y los conjuntos de hileras a ser reconocidos en el problema anterior. Esto sugiere que con pocos cambios en el conjunto de quintuplos del problema anterior podemos resolver este nuevo problema. Y así es, en efecto. Suponiendo que el estado final de aceptación será ahora el estado “7”, el conjunto de quintuplos que logrará la nueva tarea es el siguiente (se destacan en fondo amarillo el quintuplo que ha sido modificado y el quintuplo que ha sido agregado):
(0,b,b,6,D)
(0,0,X,1,D)
(1,0,0,1,D)
(1,1,1,1,D)
(1,X,X,2,I)
(1,b,b,2,I)
(2,1,X,7,I)
(3,1,1,3,I)
(3,0,0,4,I)
(3,X,X,5,D)
(4,0,0,4,I)
(4,X,X,0,D)
(5,X,X,6,D)
(7,1,X,3,I)
PROBLEMA: Encuéntrese una máquina Turing que sea capaz de poder reconocer el conjunto de todas las hileras unarias (hileras formadas por “unos”) que consistan de un número par de “unos”, lo cual incluye a la hilera vacía (sin “unos”).
La máquina Turing pedida debe poder reconocer hileras tales como:
11
1111
111111
11111111
que contienen una cantidad par de “unos”. Suponiendo que la cabeza lectora se encuentra posicionada en el extremo izquierdo de la cinta, y que las hileras de “unos” están acotadas en ambos extremos de la cinta por bits en blanco “b” que no contienen información, entonces si llamamos al estado “2” el estado final de la máquina Turing, estado al cual solo puede llegar cuando ha reconocido las hileras unarias formadas por un número par de “unos”, un conjunto de quintuplos que puede reconocer tales hileras es el siguiente (este es un problema sencillo, obsérvese que no es necesario que la cabeza lectora se mueva en sentido contrario de derecha a izquierda para llevar a cabo este procesamiento Turing):
| (0,b,b,2,D) | Este quintuplo se encarga de manejar el caso en el cual se tiene una cinta en blanco donde ya no hay más "unos" habiéndose llegado al estado final 2 ya sea porque se terminó de leer un número par de "unos" o porque no hay nada más para leer (ningún "1") |
| (0,1,1,1,D) | Este quintuplo es usado cuando se ha leido un número impar de "unos" |
| (1,1,1,0,D) | Este quintuplo es usado cuando se ha leido un número par de "unos" |
El lector deberá convencerse a sí mismo usando algunas hileras de prueba como 1, 11, 111 y 1111 y comenzando con la cabeza lectora posicionada en el “1” situado más a la izquierda que si se lee un número par de “unos” entonces la máquina se detendrá en el estado “1”, el cual no es un estado final de aceptación, mientras que si se lee un número par de “unos” entonces la máquina se detendrá en el estado “2”, el cual es un estado final de aceptación de la hilera cumpliendo la condición de que contenga un número par de “unos”.
PROBLEMA: Encuéntrese una máquina Turing que sea capaz de poder reconocer el conjunto de todos los paréntesis “bien balanceados”. Una hilera de paréntesis bien balanceados es la siguiente:
(( )(( )))
mientras que una hilera de paréntesis mal balanceados es la siguiente:
(( )(( ))
Hay varias maneras de diseñar una máquina Turing que pueda lograr lo que se está pidiendo. Supondremos que el alfabeto de símbolos incluye al símbolo “X” que irá marcando en forma intermedia cada par de paréntesis que vayan siendo apareados exitosamente. Si convenimos en llamar al estado final de aceptación de un paréntesis bien balanceado el estado “3”, entonces comenzando la lectura de la hilera de paréntesis con la cabeza lectora posicionada en el símbolo de paréntesis que está situado más a la izquierda, y suponiendo que las hileras de “unos” están acotadas en ambos extremos de la cinta por bits en blanco “b” que no contienen información, un conjunto de quintuplos que puede reconocer las hileras de paréntesis bien balanceados llegando al estado final de aceptación “3” es el siguiente:
| (0,(,(,0,D) (0,),X,1,I) (0,X,X,0,D) |
Este trio de quintuplos busca el paréntesis ")" que está situado más a la izquierda, reemplazándolo con un símbolo "X" |
| (0,b,b,2,I) | Este quintuplo es usado cuando ya no hay más paréntesis "}" |
| (1,(,X,0,D) (1,X,X,1,I) |
Este par de quintuplos es usado para buscar un paréntisis "(" para aparear |
| (2,X,X,2,D) (2,b,b,3,D) |
Al no haber más paréntesis "(", la máquina se detiene aceptando la hilera de paréntesis bien balanceados |
De nueva cuenta, es importante que el lector forme algunas hileras de paréntesis bien balanceados y otras hileras de paréntesis mal balanceados, y empezando con la cabeza lectora posicionada en el primer paréntesis situado más a la izquierda, aplicando los quintuplos que sean relevantes al pasar de un estado a otro se convenza a sí mismo de que la máquina Turing aceptará hileras de paréntesis bien balanceados y no aceptará hileras de paréntesis mal balanceados.
PROBLEMA: Encuéntrese una máquina Turing que sea capaz de poder reconocer las hileras que formen parte del conjunto de hileras 02n1n22n.
Algunas hileras que formarán parte del conjunto aceptable de hileras de acuerdo a la condición impuesta es el siguiente:
00122
0000112222
000000111222222
Mediante notación propia de la teoría de conjuntos, podemos describir de una manera un poco más elegante y formal el conjunto de hileras que queremos reconocer con la ayuda de una máquina Turing:
{ 02n1n22n | n ≥ 0 }
Hay varias maneras de diseñar una máquina Turing que pueda lograr lo que se está pidiendo. Supondremos que el alfabeto de símbolos incluye tres símbolos adicionales: “X”, “Y” y “Z”, con el propósito de ir marcando en forma intermedia los apareamientos que se vayan logrando. Este problema confirma la conveniencia de poder contar con símbolos adicionales en el alfabeto que puedan ser leídos por la cabeza lectora y que puedan ser usados para ir logrando resultados intermedios que nos acercan al objetivo final. La máquina Turing que se propondrá aquí tiene nueve estados, y será el estado “9” el estado final de aceptación que al ser alcanzado confirmará la aceptación de una hilera como parte del conjunto de hileras especificado. Un conjunto de quintuplos que puede reconocer las hileras deseadas es el siguiente:
| (0,b,b,9,D) | Este quintuplo se encarga del caso en el cual se tiene la hilera vacía, o sea una cinta que es esencialmente una cinta en blanco |
| (0,0,0,0,D) (0,1,X,1,D) |
Este par de quintuplos busca y encuentra el primer "1" que haya tras un "0", marcándolo con una "X" |
| (1,1,1,1,D) (1,Y,Y,1,D) |
Este par de quintuplos busca hacia la derecha un "2" pasando por encima de las "Y" en donde las vaya encontrando |
| (1,2,Y,3,D) (3,2,Y,4,I) |
Este par de quintuplos encuentra un par de "2", marcándolos con "Y" |
| (4,Y,Y,4,I) (4,X,X,4,I) (4,1,1,4,I) (4,Z,Z,4,I) |
Con este cuádruple de quintuplos la cabeza lectora se va moviendo hacia la izquierda buscando un "cero" |
| (4,0,Z,5,I) (5,0,Z,6,D) |
Este par de quintuplos se encarga de un par de ceros, marcándolos con un símbolo "Z" |
| (6,Z,Z,6,D) (6,X,X,6,D) (6,1,X,1,D) |
Con este trio de quintuplos, la cabeza lectora se va moviendo hacia la derecha hasta llegar al siguiente "1" |
| (6,Y,Y,7,D) | Con este quintuplo, la cabeza lectora se va moviendo hacia la derecha hasta que no hay más "unos" |
| (7,Y,Y,7,D) (7,b,b,8,I) |
Con este par de quintuplos, la cabeza lectora se va moviendo hacia la derecha hasta que no hay más "2"s |
| (8,Y,Y,8,I) (8,X,X,8,I) (8,Z,Z,9,I) (8,b,b,9,I) |
Con este cuádruple de quintuplos, al no encontrar más ceros la cabeza lectora se detiene, y la máquina llega al estado final de aceptación "9" |
Es importante que el lector forme algunas hileras diversas empezando con la cabeza lectora posicionada en el primer paréntesis situado más a la izquierda, aplicando los quintuplos que sean relevantes al pasar de un estado a otro, y se convenza a sí mismo de que la máquina Turing aceptará hileras de paréntesis que forman parte del conjunto indicado; esta es la única manera en la cual el lector podrá comprender el propósito de la acción combinada de todos los quintuplos que es a su vez el paso indispensable para poder diseñar máquinas Turing más sofisticadas.
PROBLEMA: Encuéntrese una máquina Turing que sea capaz de poder reconocer las hileras de palabras binarias tales que formen parte del conjunto dado por p*pR en donde pR es la hilera inversa a la hilera p.
En este problema no hay restricción alguna sobre la forma que tomará la hilera binaria p, lo importante es que el conjunto de palabras que se desea reconocer con una máquina Turing esté dado por p*pR siendo pR la hilera inversa a la hilera p. De este modo, si la hilera p es 111001, la hilera pR será la hilera inversa, 100111, y la hilera compuesta será:
p * pR = 111001*100111
Obsérvese que el símbolo del asterisco (*) forma parte del alfabeto de símbolos reconocidos por la cabeza lectora de la máquina. De cualquier modo, ese símbolo en sí es irrelevante, y puede ser ignorado en el procesamiento Turing de la hilera puesto que lo relevante es determinar si la hilera es una hilera compuesta formada por una palabra binaria cualquiera seguida por una palabra de la misma extensión formada por el inverso de la palabra binaria. Con quintuplos como:
(1,*,*,1,D)
(3,*,*,3,I)
(4,*,*,4,D)
se puede pasar simplemente por encima del símbolo asterisco sin hacer nada sobre el mismo, ignorándolo del mismo modo en el que son ignorados los comentarios puestos en los programas de computación que son puestos entre delimitadores para indicarle a la máquina que ignore tales comentarios.
Hay varias maneras de diseñar una máquina Turing que pueda lograr lo que se está pidiendo. La máquina Turing que se propondrá aquí tiene siete estados, y será el estado “7” el estado final de aceptación que al ser alcanzado confirmará la aceptación de una hilera como parte del conjunto de hileras especificado. Un conjunto de quintuplos que puede reconocer las hileras deseadas es el siguiente:
| (0,0,b,1,D) | Este quintuplo se encarga del "0" que está más a la izquierda, en caso de que lo haya, removiéndolo y con una "b" poniendo en blanco el espacio que ocupaba dicho cero |
| (1,0,0,1,D) (1,1,1,1,D) (1,*,*,1,D) (1,b,b,2,I) |
Este cuádruple de quintuplos va moviendo la cabeza lectora hasta encontrar el extremo derecho |
| (2,0,b,3,I) | Al encontrarse una pareja para hacer el complemento, se borra el símbolo derecho "0" reemplazándolo con una "b" y cambiando de estado |
| (3,0,0,3,I) (3,1,1,3,I) (3,*,*,3,I) (3,b,b,0,D) |
Con este cuádruple de quintuplos el propósito es encontrar el extremo izquierdo de la hilera compuesta para volver a comenzar de nuevo |
| (0,1,b,4,D) | Este quintuplo se encarga del caso en el que el "1" es el símbolo que está más a la izquierda |
| (4,0,0,4,D) (4,1,1,4,D) (4,*,*,4,D) (4,b,b,5,D) |
Este cuádruple de quintuplos se encarga de ir moviendo la cabeza lectora hasta llegar al extremo derecho de la hilera |
| (5,1,b,3,I) | Al encontrarse una pareja para hacer el complemento, se borra el símbolo derecho "1" reemplazándolo con una "b" y cambiando de estado |
| (0,*,*,6,D) | Este quintuplo se encarga del caso en el cual la palabra binaria a la izquierda del símbolo asterisco está vacía |
| (6,b,b,7,D) | Este quintuplo se encarga del caso en el cual la palabra binaria a la derecha del símblo asterisco está vacía, y siendo así, no hay más unos ni ceros pendientes de ser procesados, y por lo tanto la máquina es puesta en el estado final de aceptación "7" |
Antes de dejar este problema, resulta instructivo aclarar cierta notación matemática que se encuentra en algunos textos que tratan el tema de la máquina de Turing, y tiene que ver con las palabras binarias que pueden ser formadas por cualquier combinación finita de “unos” y “ceros” puestos en cualquier orden. Sea A un conjunto cuyos elementos son llamados símbolos y siendo A un alfabeto. Una hilera o palabra sobre A es una secuencia finita de símbolos de A. Por lo tanto, si A.=.{a,b}, entonces aabaab, bababbaa y bbbaaaa todas son hileras sobre A. El número de símbolos en una hilera es llamado su longitud. Permitimos también una hilera de longitud cero, una hilera sin símbolos, llamada la hilera vacía, a la cual simbolizaremos como λ. Llamamos a A* el conjunto de todas las hileras sobre A. Si A.=.{0,1}, entonces A*.=.{0,1}* simboliza el conjunto de todas las hileras que se pueden formar tomando los dos símbolos “0” y “1” del conjunto A, y por lo tanto hileras tales como 0110101, 100010 y 10101011 forman parte del conjunto A*. Con esta notación, podemos de una manera más formal y elegante simbolizar el conjunto de hileras en este problema que deseamos que reconozca una máquina Turing como:
{ p*pR | p ε{0,1}* y pR es la hilera reversa de p}
PROBLEMA: Encuéntrese una máquina Turing que sea capaz de poder reconocer las hileras de palabras binarias tales que formen parte del conjunto dado por p1*p2 en donde:
p1 ≠ p2
La máquina Turing pedida de poder reconocer hileras tales como:
1*0
100*010001
10110011*001000
en donde la palabra binaria que está a la izquierda del símbolo asterisco es diferente de la palabra binaria que está a la derecha del símbolo asterisco.
Hay varias maneras de diseñar una máquina Turing que pueda lograr lo que se está pidiendo. La máquina Turing que se propondrá aquí tiene ocho estados, y será el estado “8” el estado final de aceptación que al ser alcanzado confirmará la aceptación de una hilera como parte del conjunto de hileras especificado. Suponiendo que la cabeza lectora se encuentra posicionada en el extremo izquierdo de la cinta, y que las hileras de “unos” están acotadas en ambos extremos de la cinta por bits en blanco “b” que no contienen información, un conjunto de quintuplos que puede reconocer las hileras deseadas es el siguiente::
| (0,0,b,1,D) | Este quintuplo se encarga de leer el "0" que está a la izquierda de p1 removiéndolo y poniendo una "b" en el espacio que ocupaba dicho cero |
| (1,0,0,1,D) (1,1,1,1,D) (1,*,*,2,D) |
Este trio de quintuplos va moviendo la cabeza lectora hacia el la posición en donde está el símbolo asterisco |
| (2,X,X,2,D) | Con este quintuplo la cabeza lectora se irá moviendo sin detenerse hacia la derecha pasando sobre los símbolos "X" |
| (2,1,1,8,D) (2,b,b,8,D) |
Se llega con esto a una de las condiciones en las cuales las dos palabras binarias son diferentes, en cuyo caso la máquina se detiene y acepta la hilera combinada |
| (2,0,X,3,I) | Apareamiento exitoso de dos símbolos derechos |
| (3,X,X,3,I) (3,*,*,4,I) |
Con este par de quintuplos la cabeza lectora se va moviendo hacia la izquierda hasta llegar al símbolo asterisco |
| (4,1,1,4,I) (4,0,0,4,I) (4,b,b,0,D) |
Con este trio de quintuplos se va buscando el símbolo que esté situado en el extremo izquierdo |
| (0,1,b,5,D) | Con este quintuplo se lee un "1" que esté situado a la izquierda de p1 borrándolo y cambiando de estado |
| (5,0,0,5,D) (5,1,1,5,D) (5,*,*,6,R) |
Con este trio de quintuplos la cabeza lectora se va moviendo hacia la derecha hacia el símbolo asterisco, y al llegar al mismo la máquina cambiará de estado |
| (6,X,X,6,D) | Con este quintuplo, la cabeza lectora se va moviendo hacia la derecha pasando por encima de los símbolos "X" |
| (6,0,0,8,D) (6,b,b,8,D) |
Se llega con esto a una de las condiciones en las cuales las dos palabras binarias son diferentes, en cuyo caso la máquina se detiene y es puesta en el estado final de aceptación |
| (6,1,X,3,I) | Con este quintuplo, al haberse encontrado un apareamiento de símbolos se imprime un símbolo "X" |
| (0,*,*,7,D) | La palabra a la izquierda del símbolo asterisco es ya una palabra vacía |
| (7,X,X,7,D) (7,0,0,8,D) (7,1,1,8,D) |
La palabra a la derecha del símbolo asterisco no es una palabra vacía. Por lo tanto, la máquina llega al estado final de aceptación y se detiene |
| (0,b,b,0,D) | Este quintuplo se requiere para poder manejar el caso en el que la palabra p1 está inicialmente vacía |
Como una variante de este tipo de problemas en los cuales la máquina Turing es capaz de poder llevar a cabo un reconocimiento haciéndonoslo saber al llegar a un estado final de aceptación, podemos considerar el problema de encontrar una máquina Turing que sea capaz de convertir una hilera de “ceros” y “unos” que representa un número binario en una hilera que tenga esa cantidad de “unos”. Tal máquina podría tomar de la cinta un número binario como:
···bb100bb···
que en el sistema decimal es el número 4, y poner en la cinta la hilera:
···bb1111bb···
que contiene cuatro “unos”. Una estrategia para poder diseñar este tipo de máquina Turing (que equivale a encontrar el conjunto de quintuplos con el cuala será programada) es la siguiente: Poner algún símbolo marcador (por ejemplo, el símbolo asterisco) a la derecha de la hilera original p1 que representa el número binario, e ir construyendo una nueva hilera p2 a la derecha de dicho número. Trabajando dede el orden bajo de p1 (el bit menos significativo), para cada nuevo símbolo de p1 que se vaya recorriendo poner un bloque de símbolos al final de p2 que sea dos veces más grande que el bloque previo de símbolos añadidos a p2. Cuando todos los símbolos en p1 hayan sido procesados, borramos la hilera original p1 y el símbolo delimitador que sirvió para separar ambas hileras. Trabajando de izquierda a derecha sobre p2, reemplazamos cualesquier “cero” que hubiera con “unos” del final de la hilera hasta que ya no haya más “ceros” en la hilera p2, que contendrá una cantidad de “unos” igual al número binario codificado inicialmente en la hilera p2.
PROBLEMA: Encuéntrese una máquina Turing que, dada una cinta que inicialmente contenga una hilera no-vacía de “unos”, marque el extremo derecho de dicha hilera con un símbolo asterisco, y ponga una copia de dicha hilera a la derecha del símbolo asterisco.
Este problema consiste esencialmente en tomar una hilera “unos” de la cinta y hacer una copia idéntica de dicha hilera de “unos” poniendo dicha copia a un lado de la hilera original. En su quintaesencia, esto es lo que hacen muchos sistemas operativos y programas de aplicación cuando toman un archivo (que es una gran hilera de “unos” y “ceros”) y ponen una copia del archivo en algún otro lado de la máquina, con la diferencia de que la copia consta de “unos” y “ceros” y no únicamente de “unos”. La máquina Turing que estamos diseñando aquí puede empezar, por ejemplo, con una cinta que contiene la hilera:
···bb1111111bb···
y al llegar a su estado final de aceptación la cinta contendrá la hilera:
···bb1111111*1111111bb···
Existen varias maneras (y no una sola) de lograr este objetivo, y una de ellas es mediante el siguiente conjunto de quintuplos suponiendo como lo hemos estado haciendo que la cabeza lectora se encuentra posicionada en el extremo derecho de la cinta en el primer “uno” que no es un espacio en blanco, y suponiendo que el estado final de aceptación es el estado 6:
| (0,1,X,1,D) | Este quintuplo se encarga de leer el "1" que está en el extremo izquierdo de la hilera original poniendo un símbolo intermedio "X "en su lugar |
| (1,1,1,1,D) (1,b,*,2,D) (1,*,*,2,D) (2,1,1,2,D) (2,B,1,3,I) |
Llevar el "1" que fue encontrado hasta el lado derecho de la nueva hilera que está siendo formada (la copia) para pegar dicho "1" en la nueva hilera |
| (3,1,1,3,I) (3,*,*,4,I) (4,1,1,4,I) (4,X,X,0,D) |
Con este cuádruple de quintuplos se localiza el "1" más a la izquierda que se encuentre en la hilera original |
| (0,*,*,5,I) (5,X,1,5,I) (5,b,b,5,D) |
Al llegar a este punto todos los "1" de la hilera original han sido copiados, quedando por llevar a cabo el cambio de todos los símbolos temporales "X" a los "1" que había, reestableciendo la hilera original a su condición de "unos" sin símbolo "X" alguno |
No se dará aquí una simulación dinámica del conjunto de quintuplos de este problema en el cual se elabora la copia idéntica de una hilera de inicio en virtud de que es posible encontrar en Internet simulaciones de máquinas Turing de distintos grados de complejidad que pueden ser “programadas” (proporcionándoles el conjunto de quintuplos y la hilera de inicio) para efectuar el procesamiento Turing a la vista del programador (es posible que se requiera algún cambio en la notación de los quintuplos en el orden utilizado para representar los estados y los símbolos de entrada y salida, pero tales cambios son irrelevantes porque al final el resultado es lo que importa). Se recomienda al lector visitar tales sitios para acostumbrarse a “programar” con naturalidad máquinas Turing viendo el resultado de cada procesamiento paso-a-paso.